Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
3.3 Historical Comment
We have already pointed out the similarity between the inflationary
phase and the de Sitter spacetime. A closer similarity exists between
some of the ideas invoked in inflation and the steady state model
(16,
55).
In the steady state model, a steady exponential expansion [with
( / a) = constant] was
made compatible with a constant density of
matter (
/ a) = constant] was
made compatible with a constant density of
matter ( = constant)
by invoking the continuous creation of matter.
Where did this matter come from?
= constant)
by invoking the continuous creation of matter.
Where did this matter come from?
McCrea (78) had proposed negative stresses in vacuum to provide the required energy tensor to drive the expansion. In the 1950s, particle physics had not advanced to the sophisticated levels of today and so McCrea's phenomenological ideas were largely ignored by physicists. Today we can view them with greater sympathy.
An alternative theory based on Hoyle's earlier ideas of a cosmological field creating matter (55, 56) was investigated further by Hoyle & Narlikar (57, 58, 59, 60). This involved a scalar C-field, whose action function was first proposed by Pryce (103; private communication). The C-field action had two terms as part of the overall Hilbert action:
of which the first, pure field term had a negative energy density and
negative stresses for the coupling constant f > 0. This was
responsible for driving the expansion. The second, field-matter
interaction term, involving the effect of the C-field on matter
particles (labelled by a, b, . . .) and vice versa, came into operation
only at the instant of creation of matter.
The advantage of the formulation by Pryce was that it is based on an
action principle and hence guarantees conservation of matter and
energy. In the steady state solution, matter creation is compensated
by augmentation of the strength of the C-field, which has negative
energy. In this solution the Hubble constant is given by
There were also solutions of this theory with no creation of matter,
however. What role did they have to play? Hoyle & Narlikar
(59) argued
that these solutions appear as ``bubbles'' in a highly dense steady
state universe with H >> H0, the present value
of Hubble's
constant. The mechanism of the switch-over from a ``creation'' to
``noncreation'' mode was left undiscussed for want of a quantum field
theory of the C-field.
Thus, the key idea of the inflationary scenario of the present FRW
model originating as a bubble in an external de Sitter type universe
was anticipated 15 years earlier. The 1966 version [like McCrea's
(78)
1951 paper] appeared too far ahead of its time to be appreciated
by the contemporary particle physicists.
Finally, the cosmic baldness conjecture had also been anticipated by
the steady state cosmology
(57),
which argued that the C-field driven
expansion would wipe away any initial departures from nonuniformity.
In later years, other papers discussed the idea of inflation before
or around the time of Guth's paper. For example, Kazanas
(67)
explicitly discussed the notion of inflation as a solution to the
horizon problem. Kazanas assumed a temperature-dependent energy
density of the vacuum and showed that during the phase transition, the
universe would expand substantially faster than the a
Sato (107)
also discussed the implications of a first order phase
transition of vacuum in the very early universe, and obtained the
exponential expansion rate. Sato calculated the bubble nucleation
rate, which depends on the particle physics theory used. He found that
if the nucleation rates are small and the vacuum stays at the
metastable state for a long enough time, the universe would expand
exponentially, with the result that the phase transition would be
further stretched out in time. Sato also considered the possibility of
density and velocity fluctuations created by the phase transition
growing to form galaxies.
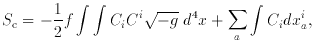
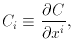
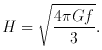
 t1/2 law. For
some temperature-dependent vacuum energies Kazanas obtained an
exponential expansion law.
t1/2 law. For
some temperature-dependent vacuum energies Kazanas obtained an
exponential expansion law.