Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
The most attractive feature of inflation, from the point of view of an astronomer, is the possibility that inflation may provide the seed perturbations that grow to form the structures we see today. In this section we provide an overview of how this is achieved and what difficulties arise.
We have discussed in Section 3.1 how inflation may lead to seed perturbations. To construct a working model from these ideas, we must (a) have a scenario that produces the observed structures from seed - perturbations and decide on the form of the seed perturbations needed, and (b) compute explicitly the nature of perturbations produced by inflation. A comparison of the outcomes of (a) and (b) will decide the measure of success achieved by inflation.
The first task can be achieved in principle by determining  (x, t0)
today observationally and extrapolating it backwards theoretically. In
practice, of course, this is an impossibly difficult task! The
structures seen today are the result of very complicated nonlinear
evolution in the ``recent'' past (say 0 < z < 50), and we do not have a
sufficiently well-defined theoretical formalism to allow us to
extrapolate back in time. (Neither do we know
(x, t0)
today observationally and extrapolating it backwards theoretically. In
practice, of course, this is an impossibly difficult task! The
structures seen today are the result of very complicated nonlinear
evolution in the ``recent'' past (say 0 < z < 50), and we do not have a
sufficiently well-defined theoretical formalism to allow us to
extrapolate back in time. (Neither do we know  (x,
t0) to sufficient
accuracy.) An indirect approach to this problem is, therefore,
necessary.
(x,
t0) to sufficient
accuracy.) An indirect approach to this problem is, therefore,
necessary.
We know from observations of MBR that the density perturbations in
the universe must have been quite small (<< 1) at the time of
decoupling (z  103), for all astrophysically relevant scales
(27,
96,
128).
We also notice from Equation 16 that all these relevant
scales ``entered the Hubble radius'' in the radiation-dominated era,
i.e. before decoupling. It follows that the linear approximation is
valid when the density perturbations enter the Hubble radius. One can,
therefore, characterize the density perturbations completely by giving
the amplitude (<< 1) of each perturbation when it enters the Hubble
radius. In other words, we need to specify the function
103), for all astrophysically relevant scales
(27,
96,
128).
We also notice from Equation 16 that all these relevant
scales ``entered the Hubble radius'' in the radiation-dominated era,
i.e. before decoupling. It follows that the linear approximation is
valid when the density perturbations enter the Hubble radius. One can,
therefore, characterize the density perturbations completely by giving
the amplitude (<< 1) of each perturbation when it enters the Hubble
radius. In other words, we need to specify the function
where tenter (k) is the time at which the
perturbation labeled by k
enters the Hubble radius decided by the equation 2
The study of the linear perturbation theory allows us to evolve
further a perturbation that enters the Hubble radius (see e.g.
98,
102).
Perturbations with
where M is the mass carried by the particular perturbation. Scales
with
The quantity k3 |
Some constraints on the form and amplitude of this spectrum can be
obtained from the bounds on the temperature anisotropies of MBR. A
perturbation of size
Zeldovich and, independently, Harrison had argued, based on
theoretical considerations, that at the time of entering the Hubble
radius, the perturbations should have the index n = -3
(51,
134). In
other words, F (k)
Three points need to be stressed regarding the above discussion.
First, note that k3 |
 k-1 a
(tenter) = cH-1 (tenter).
[Here most physical quantities depend only on the magnitude k
= |k|; in such a situation, we simplify notation by writing, say
k-1 a
(tenter) = cH-1 (tenter).
[Here most physical quantities depend only on the magnitude k
= |k|; in such a situation, we simplify notation by writing, say
 (k, t), instead
of
(k, t), instead
of  (k, t),
etc. We may also use
(k, t),
etc. We may also use  k to denote the same
quantity as was done earlier.]
k to denote the same
quantity as was done earlier.]
 <
<  eq
eq  13 Mpc (
13 Mpc ( h2)-1
h2)-1
 2, carrying mass
Meq = 3.19 x 1014 M
2, carrying mass
Meq = 3.19 x 1014 M (
( h2)-2
h2)-2  6, enter the Hubble
radius in the
radiation-dominated era; they grow by a small factor S - about
O(10)
or so - until t = teq and grow in proportion
with a (t)
afterwards. Those perturbations with
6, enter the Hubble
radius in the
radiation-dominated era; they grow by a small factor S - about
O(10)
or so - until t = teq and grow in proportion
with a (t)
afterwards. Those perturbations with  >
>  eq
enter the Hubble radius
when the universe is matter-dominated and will grow as a (t) if the
wavelength is bigger than the Jeans length. (For the scales in which
we are interested, this condition is usually satisfied). Taking F (k) =
eq
enter the Hubble radius
when the universe is matter-dominated and will grow as a (t) if the
wavelength is bigger than the Jeans length. (For the scales in which
we are interested, this condition is usually satisfied). Taking F (k) =
 kn, one can
easily work out
kn, one can
easily work out  (k, t)
for all k at t > teq. We obtain
(k, t)
for all k at t > teq. We obtain
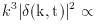
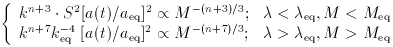
 >
cH-1 (t) are still outside the Hubble radius at
this time; it
can be shown that they grow as a2(t) in the
radiation phase and as
a (t) in the matter dominated era; they also satisfy the scalings given
above for
>
cH-1 (t) are still outside the Hubble radius at
this time; it
can be shown that they grow as a2(t) in the
radiation phase and as
a (t) in the matter dominated era; they also satisfy the scalings given
above for  >
>  eq (see e.g.
98).
eq (see e.g.
98).
 k|2 is directly related to the
r.m.s. fluctuation
in the mass M (R) contained in a size R. For a power-law spectrum
|
k|2 is directly related to the
r.m.s. fluctuation
in the mass M (R) contained in a size R. For a power-law spectrum
| k|2
k|2  kn, it can be
easily seen that the average value of <(
kn, it can be
easily seen that the average value of <( M / M)2) in
a region of size R is proportional to k3 |
M / M)2) in
a region of size R is proportional to k3 | k|2 at
k = R-1. Therefore
(
k|2 at
k = R-1. Therefore
( M / M)2
M / M)2  M-(n+3)/3 for
M < Meq and (
M-(n+3)/3 for
M < Meq and ( M / M)2
M / M)2  M-(n+7)/3 for M >
Meq.
M-(n+7)/3 for M >
Meq.
 will
produce anisotropies in the MBR at angular
scale
will
produce anisotropies in the MBR at angular
scale 
 0.55'
0.55'  h (
h ( / 1
Mpc) (see e.g.
98).
A scale of
/ 1
Mpc) (see e.g.
98).
A scale of  H = 65 (
H = 65 ( h2)-1/2
Mpc, subtending an angle of
h2)-1/2
Mpc, subtending an angle of  H
H  0.870
0.870  1/2 (zdec / 1100)-1/2, will be
entering the Hubble radius at the time of decoupling t =
tdec. Temperature anistropies in MBR at larger angles
(
1/2 (zdec / 1100)-1/2, will be
entering the Hubble radius at the time of decoupling t =
tdec. Temperature anistropies in MBR at larger angles
( >
>  H
H  10)
arise from perturbations that are still outside the Hubble radius at t
= tdec and are due to Sachs-Wolfe effect: (
10)
arise from perturbations that are still outside the Hubble radius at t
= tdec and are due to Sachs-Wolfe effect: ( T / T)
T / T)  0.5
0.5  (k, tdec)
(106).
Fluctuations at smaller scales are due to baryons that are coupled to
photons: (
(k, tdec)
(106).
Fluctuations at smaller scales are due to baryons that are coupled to
photons: ( T / T)
T / T)  0.33
0.33  baryon (k, tdec) (see e.g. 66
and references
cited therein). Bounds on (
baryon (k, tdec) (see e.g. 66
and references
cited therein). Bounds on ( T
/ T) from (1°-30°) imply that
T
/ T) from (1°-30°) imply that 
 10-4 at
scales corresponding to (65-3000)h-1 Mpc today. Such a
uniformity
suggests that (n + 3)
10-4 at
scales corresponding to (65-3000)h-1 Mpc today. Such a
uniformity
suggests that (n + 3)  -0.1. One can also show that if
-0.1. One can also show that if 
 O(1)at M
O(1)at M  1015 g
1015 g  3 x 10-19 M
3 x 10-19 M , there will be far too many
compact black holes
today, thus suggesting (n + 3)
, there will be far too many
compact black holes
today, thus suggesting (n + 3)  0.2
(21,
22).
These considerations
therefore favor (n + 3) = 0, i.e. a n = - 3 spectrum with the
amplitude of about 10-6-10-4 when each
perturbation enters the Hubble radius.
0.2
(21,
22).
These considerations
therefore favor (n + 3) = 0, i.e. a n = - 3 spectrum with the
amplitude of about 10-6-10-4 when each
perturbation enters the Hubble radius.
 |
| (k,
tenter (k))|2
(k,
tenter (k))|2  k-3 or
K3 F (k) should be a constant. In
that case <(
k-3 or
K3 F (k) should be a constant. In
that case <( M /
M)2> will be independent of the scale R at
t = tenter (k),
giving equal power at all scales at the instant of entering the horizon.
M /
M)2> will be independent of the scale R at
t = tenter (k),
giving equal power at all scales at the instant of entering the horizon.
 (k, t)|2 is not expected to be
scale-invariant
(in fact, it will not be); it is only the quantity k3
|
(k, t)|2 is not expected to be
scale-invariant
(in fact, it will not be); it is only the quantity k3
| [k,
tenter (k)]|2
that is expected to be independent of k. That is, each scale enters
the Hubble radius with an amplitude which is independent of k; but, of
course, each scale enters at a different time tenter
(k). Second, the
excess mass at scale R is in general related to the
integrated power
spectrum and depends on |
[k,
tenter (k)]|2
that is expected to be independent of k. That is, each scale enters
the Hubble radius with an amplitude which is independent of k; but, of
course, each scale enters at a different time tenter
(k). Second, the
excess mass at scale R is in general related to the
integrated power
spectrum and depends on | (k)|2 at all 0 < k < R-1
rather than just to
power at k = R-1. Finally, theoretical
calculations are expected to
fix only |
(k)|2 at all 0 < k < R-1
rather than just to
power at k = R-1. Finally, theoretical
calculations are expected to
fix only | (k,
t)|2; the phase of
(k,
t)|2; the phase of  (k, t) is not known. This is
equivalent to supposing that [
(k, t) is not known. This is
equivalent to supposing that [ (x, t) -
(x, t) -  (t)] is a random variable
with zero mean and some specified dispersion. What is determined by
the theory is the power spectrum of. this random variable, which is
the Fourier transform of the two-point correlation function <[
(t)] is a random variable
with zero mean and some specified dispersion. What is determined by
the theory is the power spectrum of. this random variable, which is
the Fourier transform of the two-point correlation function <[ (x + y,
t) [
(x + y,
t) [ (y, t)> where the brackets denote
statistical averaging over the
random phases of
(y, t)> where the brackets denote
statistical averaging over the
random phases of  (k,
t).
(k,
t).