Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
4.3 A Critique of Inflation: Expectations and Performance
The concept of inflation enjoyed considerable popularity in the first half of the last decade, though this enthusiasm seems to have died down somewhat in recent years. Taking stock of the expectations raised by inflationary scenarios in the light of its actual performance is therefore worthwhile.
Such a discussion falls conveniently into two types of questions:
1. How serious are the original problems that the inflation was invoked to solve? What alternative explanations are possible for these difficulties and how well does inflation perform vis a vis the other solutions?
2. What are new features, good and bad, that inflationary scenarios have introduced into cosmology?
Let us start with the first set of questions. In the original version, inflation was suggested as a possible solution to the horizon, flatness, and monopole problems. Of these, the monopole problem has received considerably less attention in recent literature. The currently favored unified field theories do not lead to a monopole problem. Thus, we concentrate on the flatness and horizon problems.
It is indeed true that inflation does solve these problems if these problems were stated in a particular form: inflation can suppress the value of (kc2 / a2) term; it can also make the observed region of the last scattering surface (LSS) a causally connected domain. One should not ignore, however, certain disturbing features in the inflationary solution to these problems:
Both these problems deal with the initial conditions for our universe. Since Einstein's equations permit k = - 1, 0 or + 1 in a FRW solution, the value of k needs to be supplied as an extra input to classical theory. But the creation of the universe (i.e. physics at t < tp) needs to be understood quantum mechanically rather than classically! [It is quite possible that quantum gravitational effects make a k = 0 model highly probable (see e.g. 87]. Inflation thus tries to provide a classical answer to an inherently quantum gravitational question.
This anomaly is quite striking when we consider the horizon problem. The horizon problem exists because the integral
is finite. But do we know that it is finite? To make such a claim we
have to assume that there was a singularity at t = 0 and that we know
the behavior of a (t) arbitrarily close to t = 0. For
t < tp, quantum
gravitational effects will modify the behavior of a (t) and will
probably eliminate the singularity problem. Then, for almost all a (t)
(except for a class of functions of measure zero), the above integral
will diverge, automatically solving the horizon problem. In other
words, flatness and horizon problems owe their existence to our using
classical physics beyond its domain of validity. There are several
quantum gravitational models in which these problems are solved as an
offshoot of elimination of the singularity problem (see e.g.
82,
83,
88).
This is a possibility that did not exist in classical cosmology.
Even within the context of the inflationary models, the solutions to
these problems work only for a limited time
(40,
41,
93).
For example,
Ellis has shown how the flatness problem will resurface in the
late-time behavior of a k
[For t
Let us now consider the second question, that is, the new features
that inflation has brought into cosmology. The major success of
inflation in our opinion lies in these factors.
First, inflation has provided a mechanism that allows one, in
principle, to compute the spectrum of density inhomogeneities from
fundamental physics. This must be considered a success because this is
the first time we have a computable mechanism for producing density
inhomogeneities.
Also, a definite prediction emerges from inflationary models. The
same mechanism that produces the density inhomogeneities also produces
gravitational wave perturbations. These perturbations also have a
scale invariant power spectrum and an r.m.s. amplitude of about
(H / 1019 GeV). The energy density of the
gravitational waves
contributes a fraction
Second, several investigations have suggested that inflation could
be a generic feature of cosmology; in other words, for almost any kind
of V (
The above two features also have a negative side, discussed in
Section 4.2:
Inflation produces too much density inhomogeneity. Every
unworkable model for inflation rules out a parameter range for the
potential V (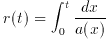
 0
universe. [This should be clear from the
fact that at sufficiently late times, both the k = + 1 and
k = - 1
models will behave very differently irrespective of the present value
of the (kc2 / a2) term.] In the case
of the horizon problem, it can be
shown that LSS will appear homogeneous only for times t <
tcrit when
0
universe. [This should be clear from the
fact that at sufficiently late times, both the k = + 1 and
k = - 1
models will behave very differently irrespective of the present value
of the (kc2 / a2) term.] In the case
of the horizon problem, it can be
shown that LSS will appear homogeneous only for times t <
tcrit when
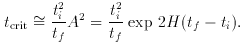
 10-34 s, tf
10-34 s, tf  100ti, H
100ti, H  (109 GeV),
tcrit
(109 GeV),
tcrit  3 x
1023 s, which
is far larger than t0
3 x
1023 s, which
is far larger than t0  3 x 1017 s; so, right now, t0
< tcrit.] This
quantity tcrit is determined once and for all by
microscopic physics at
t
3 x 1017 s; so, right now, t0
< tcrit.] This
quantity tcrit is determined once and for all by
microscopic physics at
t  10-34 s!
If we wait long enough, t will be larger than
tcrit, and
the horizon problem will resurface. Thus inflation offers only a
temporary, though long, relief from these problems, and one has to
invoke the anthropic principle
(11)
to justify its success. In
contrast, solutions based on quantum gravitational models solve these
problems permanently.
10-34 s!
If we wait long enough, t will be larger than
tcrit, and
the horizon problem will resurface. Thus inflation offers only a
temporary, though long, relief from these problems, and one has to
invoke the anthropic principle
(11)
to justify its success. In
contrast, solutions based on quantum gravitational models solve these
problems permanently.
 grav
grav  10-5 (H / mp)2
h-2 to the critical density,
where mp is the Planck mass
(1,
5,
43,
105,
129).
Such perturbations
can induce a quadrupole anisotropy in the MBR. The present bounds on
this anisotropy (
10-5 (H / mp)2
h-2 to the critical density,
where mp is the Planck mass
(1,
5,
43,
105,
129).
Such perturbations
can induce a quadrupole anisotropy in the MBR. The present bounds on
this anisotropy ( 10-4) suggest that H < 1015 GeV. The value
of
10-4) suggest that H < 1015 GeV. The value
of  grav
can also be restricted by the timing measurements of the millisecond
pulsar; the present bound is
grav
can also be restricted by the timing measurements of the millisecond
pulsar; the present bound is  grav (
grav ( ~ 1pc)
~ 1pc)  3 x 10-7. A positive
detection of quadrupole anisotropy in MBR or a direct detection of
relic gravitational radiation will certainly go a long way toward
boosting confidence in inflation. (The Laser Interferometer Gravity
Wave Observatory (LIGO) and similar projects can, in principle, reach
a sensitivity of
3 x 10-7. A positive
detection of quadrupole anisotropy in MBR or a direct detection of
relic gravitational radiation will certainly go a long way toward
boosting confidence in inflation. (The Laser Interferometer Gravity
Wave Observatory (LIGO) and similar projects can, in principle, reach
a sensitivity of  grav ~ 10-11.]
grav ~ 10-11.]
 ) and for a large
class of initial conditions, the universe will
undergo a phase of exponential expansion
(63,
64,
112,
116). The
amount of inflation, time of occurrence, etc. can all be quite varied,
but the physical phenomenon is probably here to stay (see, however,
the discussion in Section 6).
) and for a large
class of initial conditions, the universe will
undergo a phase of exponential expansion
(63,
64,
112,
116). The
amount of inflation, time of occurrence, etc. can all be quite varied,
but the physical phenomenon is probably here to stay (see, however,
the discussion in Section 6).
 ) and can, in
principle, constrain particle physics
models. This is probably the most important unsolved problem in the
physics of the early universe.
) and can, in
principle, constrain particle physics
models. This is probably the most important unsolved problem in the
physics of the early universe.