


The Planck time in cosmology is certainly the most challenging epoch to study, as the framework in which it must be described is still lacking. Though there are several different approaches to this problem, I will limit myself to that of string/M-theory [5].
Much of the work on string cosmology has focussed on the problem of inflation, and I will return to that subject in the next section. The realization that all of the different string theories, together with 11-dimensional supergravity, can be related through dualities has had a major impact on how we view the Planck epoch in cosmology. It has even led to the ultimate question as to what we mean by the Planck epoch. In a standard 4-dimensional model, the gravitational action can be written as
where
Upon reduction to 4 dimensions, we recover a relatively simple
dilaton gravity system, which for a fixed dilaton (fixed by some
potential which is perhaps induced by supersymmetry breaking), is
just Einstein gravity in 4 dimensions along with some higher
derivative curvature corrections (not shown) and additional moduli
fields (also not shown).
As noted above, M-theory is emerging as the single underlying
theory capable of unifying all particle interactions
[7].
Although our understanding of M-theory is still incomplete,
its various low energy limits, and the links between them,
are known. These are the consistent string theories and 11D
supergravity, related by dualities.
A consequence of these developments is that the dilaton
can be viewed as another modulus field in 11D
supergravity. This could have important consequences for
cosmological applications. The troubles with implementing
conventional inflationary scenarios in string theory arise because
of the dilaton and its couplings to the other modes in the string
spectrum (see below). In 11D supergravity, such
couplings are absent, and thus some of the obstacles for inflation in
dilaton-plagued string theories could
perhaps be resolved by way of M-theory.
One of the key points in the application of M theory
to phenomenology is the reconciliation of the bottom-up
calculation of MGUT ~ 1016 GeV with
the string
unification scale, which is close to the four-dimensional Planck
mass scale
M4 ~ 1019 GeV. This is achieved by
postulating a large fifth dimension
For
Within this general five-dimensional framework,
two favored ranges for the magnitude of
As a starting point therefore, one should consider the 11D supergravity action
where R is the scalar curvature of
the 11D metric (terms involving the 3-form potential and its
4-form field strength are not shown).
Reducing to 10D is done easily by assuming that the
11th direction is compact. In this case, we can carry out
Kaluza-Klein reduction of (4) to find
After a conformal rescaling
g10 =
If the 6-space is of the fundamental scale, then as described
above, the Universe will have passed through a phase where it
can be effectively described by a 5-dimensional space time.
A simple ansatz for the 5D metric is that of the FRW form
In this way, the dilaton expectation value
<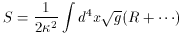
 2 =
8
2 =
8 GN =
8
GN =
8 /
MP2. In the context of a four
dimensional theory, there is nothing ambiguous here as the Planck
mass, determined from Newton's constant is simply MP =
1.2 x 1019 GeV. Even in the context of an ``old'' 10-dimensional
string theory, the 10-dimensional gravitational constant,
/
MP2. In the context of a four
dimensional theory, there is nothing ambiguous here as the Planck
mass, determined from Newton's constant is simply MP =
1.2 x 1019 GeV. Even in the context of an ``old'' 10-dimensional
string theory, the 10-dimensional gravitational constant,
 210 =
8
210 =
8 /
M108 is equivalent to its 4-dimensional
counterpart if the size of the 6-dimensional compact space is
Planck scale in extent, ie.
M10 = MP.
Of course, the gravitational action in string theory must be
augmented by the presence of additional fields in the gravitational
sector, most notably by the universal coupling of the string
dilaton [6].
Restricting our attention to only the dilaton gravity action, we can write
/
M108 is equivalent to its 4-dimensional
counterpart if the size of the 6-dimensional compact space is
Planck scale in extent, ie.
M10 = MP.
Of course, the gravitational action in string theory must be
augmented by the presence of additional fields in the gravitational
sector, most notably by the universal coupling of the string
dilaton [6].
Restricting our attention to only the dilaton gravity action, we can write
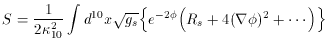
 5 >>
MGUT-1, which is
not felt by the gauge interactions, but causes the gravitational
interactions to rise with energy much faster than in the
conventional four dimensions
[7].
If we assume that the
compact 6-space (Calabi-Yau?) is of the size determined by the
fundamental Planck scale, M11 so that
V6 ~ M11-6, then the
fundamental Planck scale, M11 is
related to the four dimensional Planck scale by
M119V6
5 >>
MGUT-1, which is
not felt by the gauge interactions, but causes the gravitational
interactions to rise with energy much faster than in the
conventional four dimensions
[7].
If we assume that the
compact 6-space (Calabi-Yau?) is of the size determined by the
fundamental Planck scale, M11 so that
V6 ~ M11-6, then the
fundamental Planck scale, M11 is
related to the four dimensional Planck scale by
M119V6 5 ~
M42. Or,
5 ~
M42. Or,
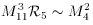
 5 >>
M11-1, it is possible to achieve
M4 >> M11 ~ MGUT.
In this type of scenario, one could expect
that inflation should be considered within a five-dimensional framework.
5 >>
M11-1, it is possible to achieve
M4 >> M11 ~ MGUT.
In this type of scenario, one could expect
that inflation should be considered within a five-dimensional framework.
 5 can be
distinguished. One is relatively close to
MGUT-1:
5 can be
distinguished. One is relatively close to
MGUT-1:
 5-1 ~
1012 to 1015 GeV, and the other could be
as low as
5-1 ~
1012 to 1015 GeV, and the other could be
as low as
 5-1 ~
1 TeV
[8].
In this latter
case, the large dimension is not necessarily the conventional fifth
dimension of M theory. Indeed, in models studied in
[8] the
large dimension may be related to what is normally considered as one
of the six ``small'' dimensions that is conventionally compactified
a là Calabi-Yau. Of course the physics of a very large
(
5-1 ~
1 TeV
[8].
In this latter
case, the large dimension is not necessarily the conventional fifth
dimension of M theory. Indeed, in models studied in
[8] the
large dimension may be related to what is normally considered as one
of the six ``small'' dimensions that is conventionally compactified
a là Calabi-Yau. Of course the physics of a very large
( 1 mm) extra spatial
dimension has received considerable attention
lately
[9,
5].
1 mm) extra spatial
dimension has received considerable attention
lately
[9,
5].
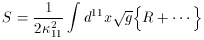
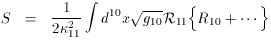
 11-1
gs, and
defining the dilaton by
exp(2
11-1
gs, and
defining the dilaton by
exp(2 / 3) =
/ 3) =
 11, we find
exactly the action given in eq. (2).
This is precisely the effective action which describes the low
energy limit of the IIA superstring (though to be sure of the
identification, one would be required to keep track of the terms
shown here as ... ). It is easy to rewrite this action in the
ten-dimensional Einstein frame, by a further conformal rescaling
gs =
e
11, we find
exactly the action given in eq. (2).
This is precisely the effective action which describes the low
energy limit of the IIA superstring (though to be sure of the
identification, one would be required to keep track of the terms
shown here as ... ). It is easy to rewrite this action in the
ten-dimensional Einstein frame, by a further conformal rescaling
gs =
e /2
gE. The action (2) can be reduced
further to make contact with type IIB and heterotic theories.
/2
gE. The action (2) can be reduced
further to make contact with type IIB and heterotic theories.
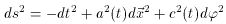
 >
is related to the scale factor c(t). In the specific case of
Horava-Witten type compactifications on S1 /
Z2, the Universe is
described by two 4D branes at the end points of the line segment.
This type of compactification is particularly well suited for
a reduction of M-theory to heterotic string theory, where the
matter and hidden sectors sit on opposing branes.
The cosmology of these theories has been studied at length in
[10].
>
is related to the scale factor c(t). In the specific case of
Horava-Witten type compactifications on S1 /
Z2, the Universe is
described by two 4D branes at the end points of the line segment.
This type of compactification is particularly well suited for
a reduction of M-theory to heterotic string theory, where the
matter and hidden sectors sit on opposing branes.
The cosmology of these theories has been studied at length in
[10].