


It has been known for quite
some time that it is very difficult to incorporate conventional
inflationary scenarios based on (de Sitter expansion) into the
low-energy limit of string theory
[11].
The principal
obstacle has been the fact that the low-energy dynamics of the theory
contains massless scalar fields with non-minimal couplings to gravity
whose coupling constants are precisely given by the conformal symmetry
and/or the dualities of string theory. In an expanding universe, these
fields roll during the course of the expansion as dictated by their
equations of motion, consuming the available energy and hence
decreasing the rate of expansion. That is, besides the Minkowski
space solution, there are no other solutions to Einstein's equations
(when the Gauss-Bonnet curvature squared terms are kept) of the
dilaton-gravity system with constant curvature and a stationary
dilaton. de Sitter solutions are possible if the dilaton sits in a
potential minimum (with V 0)
due to supersymmetry breaking
effects, but in this case, the theory suffers a graceful exit problem.
0)
due to supersymmetry breaking
effects, but in this case, the theory suffers a graceful exit problem.
Instead, one typically finds solutions where
the scale factor of the universe grows as a power of time, with the
power determined by the scalar coupling constants. Once the numerical
values of these constants, fixed by string theory, are taken into
account, it has been found that the resulting power laws are too slow
to give an inflationary universe
[12].
For example, if we ignore the compact 6-space of eq. (2) and
include a cosmological term  we have a 4D action
we have a 4D action
where now
In the Einstein frame, the solution to the equations of motion yield a
scale factor which grows linearly in time
[13].
However, this
expansion turns out not to be physical - the corresponding scale
factor in the string frame is constant. To resolve this quandary, one
must compare the scale factor in each frame with some physical length
scale, such as the Compton wavelength of a massive particle.
Had we included a massive scalar field in the action (7), we
would find that the scale factor relative to the Compton wavelength
An interesting alternative to the standard inflationary picture in
string theory is the pre-big bang scenario
[14].
The solutions
to the equations of motions in the string frame yield two
distinct branches often labeled (+) and (-) corresponding to
solutions which either evolve towards singularities and are
singularity-free in the past, or evolve from singularities and are
singularity-free in the future. One of the goals of the pre-big bang
scenario is the connection of the expanding solutions in the two
branches, in such a way that the (+)-branch chronologically precedes
the (-)-branch and hence the cosmological singularity would be
removed. It still remains to be seen if a coherent and fully
consistent description of branch-changing can be found. In fact there
are strong arguments showing the precise difficulty of a branch change
[15]
though some progress has been made to resolve this graceful exit problem
[16].
It is interesting to note that in the string frame, both
the expanding and contracting metrics are degenerate to a single
Einstein frame metric, and that the only difference between the two
subclasses of solutions is the sign of the dilaton field. In the
context of a full 11D theory, there are several solutions which can be
found [17]
all degenerate with the known pre-big bang solutions.
There is of course no possibility in this contribution to review all
of the work on inflation in the context of string theories and
extra dimensions. However, before moving to the subject of
baryogenesis, I will mention two possibilities in which extra
dimensions aid the implementation of inflation. For other recent work
see [18].
In the first
[19],
one makes use of the higher derivative curvature terms in the action.
Among the first utilizations of higher-derivative curvature terms
is the Starobinsky model
[20],
which is based on obtaining a
self-consistent solution of Einstein's equations when they are
modified to include one-loop quantum corrections to the stress-energy
tensor
Tµ
It is well known that this theory is
conformally equivalent to a theory of Einstein gravity plus a
scalar field
[22].
The potential for the resulting scalar is extremely flat for
field values
In general, quantum corrections to the right-hand side of
Einstein's equation in the absence of matter can be written as
[24]
where k2 and k3 are constants that
appear in the process of
regularization. k2 is related to the number of
light spin states, which can be very large in variants of string
theories based on M theory. On the
other hand, the coefficient k3 is independent of the
number of
light states. This term is equivalent to the variation of the
R2 term in the effective action. The theory admits a
de Sitter solution which can be found from the 00 component of
gravitational equation of motion
[25].
Defining
H' = 2880
where H is the Hubble parameter. The de Sitter
solution corresponds to H = H' and of course
In order to avoid the overproduction
of gravitons there is a lower limit on the parameters
k2, 3
[27,
26]:
k2 >> ~ 1010 implying the need for
billions of spin degrees of freedom to be present. While this seems
like an inordinately
large number, it is possible to generate very large
numbers of degrees of freedom in theories with extra dimensions.
Particularly if
N ~ MGUT
In general R2 corrections to the action do not appear
in 5 (11)
dimensions. Therefore the first correction is of order R4.
Like the curvature squared correction, the action
can be conformally transformed to a 5D Einstein theory with an
additional scalar field (
The dilaton potential here, as in most string descendent models, is
problematic unless it is fixed by an additional potential. In the
absence of a dilaton potential, this model will not inflate. The
remaining potential (of
It can be shown
[19]
that the potential (13)
does satisfy the conditions for topological inflation.
In addition, there is no problem with the graceful exit.
However, the spectrum of density fluctuations can be calculated
and the spectral index is given by
ns = 1 - m2 /
Hm2, where m2 and
Hm2 are the curvature
(of the potential) and Hubble parameter determined at the maximum.
In this model, ns = 3/8. Furthermore, the magnitude of
density fluctuations requires
Hm ~ M5 ~
10-14M4 which are probably unacceptably small.
These problems can be remedied by either the inclusion of an
R2
correction to the action, or by a large tower of KK states.
The resolution of the problem can be traced to the magnitude of the
Hubble parameter, which is determined by
H2 ~ U(
The second possibility
[30,
31],
also makes use of the
tower of KK states. The idea of using multiple fields to drive
inflation where the parameters of the theory would normally not
lead to sufficient inflation is called assisted inflation
[32].
For example, it is well known that scalar fields
with exponential potentials of the form
V(
Assistance, can in fact be generalized to other types of potentials
[30].
For example, we can
consider a general field theory of multiple, self-interacting
scalar fields of the form
This system consists
of N completely equivalent, decoupled scalar fields. As a result, the
Lagrangian can be written as
where
The resulting theory describes a single
scalar field with the same type of self-interactions compared to the
fields in the original theory. However, these self-interactions are
considerably weaker since both of the coupling constants now scale
with the number of scalar fields
N. As a result, as the number of scalar fields that we include in the
theory becomes larger, the coupling constants become smaller and the
corresponding fine-tuning becomes milder.
Thus the same basic idea expounded in
[32,
33]
carries over very simply to chaotic inflation
[23]
based on a quartic potential. While
In [30,
31],
it was suggested that the source of the
multiple fields is the KK reduction from a higher dimensional
theory to 4D. For example, the reduction of a 5D theory results in
N
When KK-reduced to 4D,
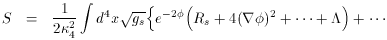
 4-2
= M42 / 8
4-2
= M42 / 8 .
In the Einstein frame this becomes
.
In the Einstein frame this becomes
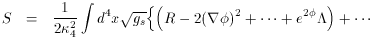
 ~ m-1 is
also constant. However, in the Einstein
frame, the mass term would also be dilaton dependent with mass
e
~ m-1 is
also constant. However, in the Einstein
frame, the mass term would also be dilaton dependent with mass
e m,
implying that the Compton wavelength also grows linearly
in time (
m,
implying that the Compton wavelength also grows linearly
in time ( ~ - ln t) and
hence relative to a physical measure
of length, the Universe according to (8) is also not expanding
[12].
~ - ln t) and
hence relative to a physical measure
of length, the Universe according to (8) is also not expanding
[12].
 . In its
simplest form, the model is equivalent
to a theory of gravity with an R2 correction which can be
written as
[21]
. In its
simplest form, the model is equivalent
to a theory of gravity with an R2 correction which can be
written as
[21]
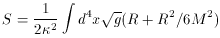
 >> M4 and has a
minimum at
>> M4 and has a
minimum at  = 0 with
V(
= 0 with
V( = 0) = 0.
For large initial values of
= 0) = 0.
For large initial values of  , one
can recognize this as an excellent model for chaotic inflation
[23].
, one
can recognize this as an excellent model for chaotic inflation
[23].
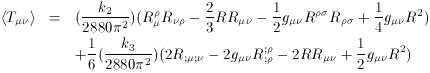
 2 /
k2 and
M2 = 2880
2 /
k2 and
M2 = 2880 2 /
k3, and setting the spatial curvature
k = 0, one finds
[26]
2 /
k3, and setting the spatial curvature
k = 0, one finds
[26]
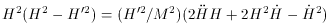
 =
=
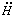 = 0.
= 0.
 5
5
 108
[19].
The bound for k3 is
k3
108
[19].
The bound for k3 is
k3  109,
corresponding to
M
109,
corresponding to
M  1014 GeV.
1014 GeV.

 ) and a
potential U(
) and a
potential U( )
[28].
Making the KK reduction to 4D, we find in addition to
)
[28].
Making the KK reduction to 4D, we find in addition to
 , a second scalar field
(
, a second scalar field
( ) which is the modulus of the
5th dimension and is related to the dilaton.
The resulting potential takes the form
[19]
) which is the modulus of the
5th dimension and is related to the dilaton.
The resulting potential takes the form
[19]
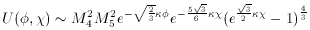
 ) differs
from that in the R2
model. As one can see it is no longer flat, but rather takes the
shape similar to that of the double well potential. As a result,
chaotic inflation
[23]
with a large initial value of
) differs
from that in the R2
model. As one can see it is no longer flat, but rather takes the
shape similar to that of the double well potential. As a result,
chaotic inflation
[23]
with a large initial value of
 is impossible
here. Nevertheless there may remain the possibility to realize
inflationary expansion in this model by using the potential energy
around the local maximum,
V(
is impossible
here. Nevertheless there may remain the possibility to realize
inflationary expansion in this model by using the potential energy
around the local maximum,
V( m), as in the
topological inflation scenario of Linde and
Vilenkin
[29].
In this scenario, if the scalar field
m), as in the
topological inflation scenario of Linde and
Vilenkin
[29].
In this scenario, if the scalar field
 (x) is randomly distributed
initially with a large dispersion, some part of the universe will roll to
(x) is randomly distributed
initially with a large dispersion, some part of the universe will roll to
 = 0, while
in other parts it will run away to infinity. Between any two such
regions there will appear domain walls, containing a large energy density,
= 0, while
in other parts it will run away to infinity. Between any two such
regions there will appear domain walls, containing a large energy density,
 ~
V(
~
V( m). If the wall
is thicker than the
Hubble radius of this energy density, there will exist a
sufficiently large quasi-homogeneous region, filled with large
potential energy, where inflationary expansion naturally sets in.
m). If the wall
is thicker than the
Hubble radius of this energy density, there will exist a
sufficiently large quasi-homogeneous region, filled with large
potential energy, where inflationary expansion naturally sets in.
 ) /
M42.
In the presence of a large number of degrees of freedom, quantum
corrections modify this relation along the line of eq.
(11) in which case H is driven to H' and need not be
exceptionally small. It suffices now that
H, M5 ~ 10-5M4
with
) /
M42.
In the presence of a large number of degrees of freedom, quantum
corrections modify this relation along the line of eq.
(11) in which case H is driven to H' and need not be
exceptionally small. It suffices now that
H, M5 ~ 10-5M4
with
 5-1 ~
O(100) GeV. In this case, the spectral
index is
5-1 ~
O(100) GeV. In this case, the spectral
index is
 0.95 and the magnitude of
fluctuations is acceptably small.
0.95 and the magnitude of
fluctuations is acceptably small.
 ) = e-
) = e-
 , lead to power law expansion with the cosmological
scale factor growing as
R(t) ~ tp and
p = 2 /
, lead to power law expansion with the cosmological
scale factor growing as
R(t) ~ tp and
p = 2 /  2. Density
fluctuations are no longer scale invariant but scale as
|ð
2. Density
fluctuations are no longer scale invariant but scale as
|ð /
/
 (k)|2 ~ kn - 1 with
n = 1 - 2/(p - 1). Sufficient inflation along with
n
(k)|2 ~ kn - 1 with
n = 1 - 2/(p - 1). Sufficient inflation along with
n  1, requires
p to be large. In
[32],
it was shown that a system of scalar fields each with exponential
potentials, (even if the individual powers, pi, are
not sufficiently
large to generate inflation) has an attractor
solution in which the universe power-law expands with a power given by
p =
1, requires
p to be large. In
[32],
it was shown that a system of scalar fields each with exponential
potentials, (even if the individual powers, pi, are
not sufficiently
large to generate inflation) has an attractor
solution in which the universe power-law expands with a power given by
p =  pi.
pi.
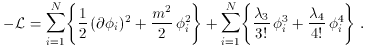
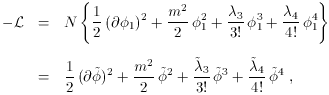
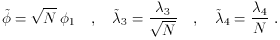
 4 must
still be of order 10-12, the fundamental coupling in
the theory
4 must
still be of order 10-12, the fundamental coupling in
the theory  4 can
now be much larger if N is large.
In addition, the problem associated with chaotic inflation
[34],
large (
4 can
now be much larger if N is large.
In addition, the problem associated with chaotic inflation
[34],
large ( >> Mp)
initial field values and the
necessary fine tuning of non-renormalizable interactions, is cured
[31].
Because of the rescaling in eq. (16), in a
theory of multiple fields, chaotic inflation will operate, even
though none of the fields have expectation values greater than
MP.
>> Mp)
initial field values and the
necessary fine tuning of non-renormalizable interactions, is cured
[31].
Because of the rescaling in eq. (16), in a
theory of multiple fields, chaotic inflation will operate, even
though none of the fields have expectation values greater than
MP.

 5
M5 fields. Though these fields are not
decoupled as in the example above, and hence assistance is not
guaranteed
[30,
35],
attractor solutions do exist and
assistance is generated primarily due to the rescaling of the
fields (from 5D to 4D) which is necessary due to the dimensional
reduction. To see this, consider the action
5
M5 fields. Though these fields are not
decoupled as in the example above, and hence assistance is not
guaranteed
[30,
35],
attractor solutions do exist and
assistance is generated primarily due to the rescaling of the
fields (from 5D to 4D) which is necessary due to the dimensional
reduction. To see this, consider the action

 G5 ->
G5 ->
 G45
and canonical 4D scalar fields must be defined by
G45
and canonical 4D scalar fields must be defined by
 =
sqrt[2
=
sqrt[2 5]
5]
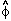 and hence the quartic potential
becomes
and hence the quartic potential
becomes

 4 /
4! with
4 /
4! with
 =
=
 /
2
/
2 5
M5 =
5
M5 =  / N.
/ N.