


The exact time period for baryogenesis is not known but most
certainly it is completed no later than the electroweak phase
transition. There are of course many mechanisms for baryogenesis
which have been proposed in the literature
[36],
too many to
be comprehensive here. All require baryon number violation, C and
CP violation, and a departure from thermal equilibrium
[37].
The original out-of-equilibrium decay (OOED) scenario
[38] is
probably still the simplest of all mechanisms. Originally
formulated in the context of grand unified theories, OOED
involved the decay of a superheavy gauge or Higgs boson with baryon
number violating couplings. For example, the X gauge boson of
SU(5) couples to both a
(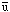
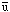 ) pair and (e-d).
The decay rate for X will be
) pair and (e-d).
The decay rate for X will be
However decays can only begin occurring when the age
of the Universe is longer than the X lifetime
The out-of-equilibrium condition is
that at T = MX,
In this case, we would expect a maximal net baryon asymmetry to be
produced, nB / s ~ 10-2
In the context of inflation, OOED requires either strong reheating
(or preheating)
[39],
or that the decaying particles have
masses less than the inflaton mass so that they can be produced
(necessarily out of equilibrium) by inflaton decays.
For example, if the inflaton potential carries only a single scale
which is fixed by the magnitude of density fluctuation as measured in
the microwave background radiation, then we can write
[40]
Typically,
so that
In this case a relatively light Higgs is necessary since the inflaton
is typically light
(m
where TR is the reheat temperature after inflation,
n
In the context of supersymmetry, there is an extremely natural
mechanism for the generation of the baryon asymmetry utilizing flat
directions of the scalar potential
[42].
One can show that
there are many directions in field space such that the scalar
potential vanishes identically
when SUSY is unbroken. That is,
One such example is
[42]
where a, v are arbitrary complex vacuum expectation values.
SUSY breaking lifts this degeneracy so that
where
When combined with inflation, it is important to verify that the AD
flat directions remain flat. In general, during inflation,
supersymmetry is broken. The gravitino mass is related to the vacuum
energy and
m3/22 ~ V /
MP2 ~ H2, thus lifting the flat
directions and potentially preventing the realization of
the AD scenario as argued in
[44].
To see this, consider a minimal supergravity model whose
Kähler potential is defined by
where z is a Polonyi-like field
[45]
needed to break
supergravity, and we denote the scalar components of the usual matter
chiral supermultiplets by
Included in the above expression for V, one finds a mass term for
the matter
fields
There is however a special class of models called no-scale
supergravity models, that were first introduced in
[47]
and have
the remarkable property that the gravitino mass is undetermined at the
tree level despite the fact that supergravity is broken.
No-scale supergravity has been
used heavily in constructing supergravity models in which all mass
scales below the Planck scale are determined radiatively
[48],
[49].
These models emerge naturally in torus
[50]
or, for the untwisted sector, orbifold
[51]
compactifications of the heterotic string.
In no-scale models (or more generally in models which possess a
Heisenberg symmetry
[52]),
the Kähler potential becomes
Now, one can write
It is important to notice that the cross term
|
which is positive definite. The requirement that the vacuum energy vanishes
implies <Wi> = <ga> = 0 at the
minimum. As a consequence
The above argument is only valid at the tree level.
An explicit one-loop calculation
[54]
shows that the
effective potential along the flat direction has the form
where
In [56],
several possible solutions were presented to dilute
the baryon asymmetry. These included 1) Moduli decay, 2) the presence
of non-renormalizable interactions, and 3) electroweak effects.
Moduli decay in this context, turns out to be insufficient to bring an
initial asymmetry of order
nB/s ~ 1 down to acceptable levels.
However, as a by-product one can show that there is no moduli problem
[57]
either. In contrast, adding non-renormalizable Planck scale
operators of the form
where the temperature
T ~ TC ~ 200 GeV is when the sphaleron
transition freezes out (similar to the temperature of the electroweak phase
transition) and
m
Finally, it is necessary to mention one other extremely simple
mechanism based on the OOED of a heavy Majorana neutrino
[59].
This mechanism does not require grand unification at all.
By simply adding to the Lagrangian a Dirac and Majorana mass term
for a new right handed neutrino state,
the out-of-equilibrium decays
Acknowledgments
As the Inner Space/Outer Space II workshop, and these proceedings
are in memory of Dave Schramm, it is fitting to acknowledge Dave's
role. Dave's research interests were predominantly concerned with the
epoch of Big Bang Nucleosynthesis and the post BBN Universe. His
research interests are known to have been extremely diverse covering
such areas as chemical evolution, cosmic rays, cosmochronology, dark
matter, galaxy formation and mergers, the gamma-ray background,
magnetic fields, mass extinctions, neutrinos, (late-time) phase
transitions, supernovae, ... In addition, he was a master at
synthesizing and finding relationships between these topics.
Though pre-BBN cosmology was not Dave's mainstay, he did of course
make important contributions in areas such as baryogenesis and
topological defects. But Dave's most important contribution was
the early recognition of the impact of cosmology on particle
physics. He can legitimately be considered a founding father of
astro-particle physics. On a more personal note, it is difficult to
put into words the immense impact that Dave has had on my research, as
an advisor, colleage, and friend. This work was supported in part by
DOE grant DE-FG02-94ER40823 at Minnesota.
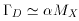
 -1D,
i.e., when
-1D,
i.e., when
 D > H
D > H
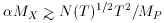
 D < H or
D < H or
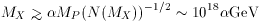
 , where
, where
 is a measure
of the CP violation in the decay.
is a measure
of the CP violation in the decay.
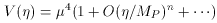
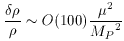
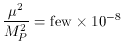
 ~ µ2 / MP ~
O(1011) GeV)
and the baryon number violating Higgs
would have to be produced during inflaton decay.
Clever model building could allow for such a light Higgs, even in the
context of supersymmetry
[41].
In this case, the baryon asymmetry is given simply by
~ µ2 / MP ~
O(1011) GeV)
and the baryon number violating Higgs
would have to be produced during inflaton decay.
Clever model building could allow for such a light Higgs, even in the
context of supersymmetry
[41].
In this case, the baryon asymmetry is given simply by
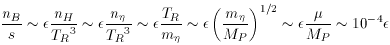
 =
=

 /
m
/
m ~
~
 2
MP2 /
m
2
MP2 /
m ,
and
,
and  =
m
=
m 3 / MP2 is the
inflaton decay rate.
3 / MP2 is the
inflaton decay rate.
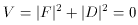
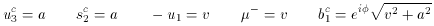
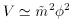
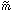 is the SUSY breaking
scale and
is the SUSY breaking
scale and  is the direction
in field space corresponding to the flat direction.
For large initial values of
is the direction
in field space corresponding to the flat direction.
For large initial values of  ,
,
 0 ~ Mgut,
a large baryon asymmetry can be generated
[42,
43].
This requires
the presence of baryon number violating operators such as O =
qqql such that
<O>
0 ~ Mgut,
a large baryon asymmetry can be generated
[42,
43].
This requires
the presence of baryon number violating operators such as O =
qqql such that
<O>  0. The decay of these
condensates through such an operator can lead to a net baryon asymmetry.
0. The decay of these
condensates through such an operator can lead to a net baryon asymmetry.
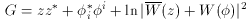
 i. W and
i. W and
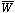 are the superpotentials of
are the superpotentials of
 i and z
respectively. In this case, the scalar potential becomes
i and z
respectively. In this case, the scalar potential becomes
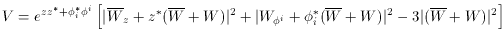
 i,
eG
i,
eG i*
i* i
= m3/22
i
= m3/22 i*
i* i
[46].
As it applies to
all scalar fields (in the matter sector), all flat directions are
lifted by it as well. The above arguments can be generalized to
supergravity models with non-minimal Kähler potentials.
i
[46].
As it applies to
all scalar fields (in the matter sector), all flat directions are
lifted by it as well. The above arguments can be generalized to
supergravity models with non-minimal Kähler potentials.
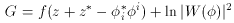
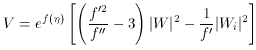
 i*W|2 has
disappeared in the
scalar potential. Because of the absence of the cross term, flat
directions remain flat even during inflation
[53].
The no-scale model corresponds to f = - 3
ln
i*W|2 has
disappeared in the
scalar potential. Because of the absence of the cross term, flat
directions remain flat even during inflation
[53].
The no-scale model corresponds to f = - 3
ln ,
f '2 = 3f'' and the first term in
(31)
vanishes. The potential then takes the form
,
f '2 = 3f'' and the first term in
(31)
vanishes. The potential then takes the form
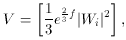
 is undetermined
and so is the gravitino mass
m3/2(
is undetermined
and so is the gravitino mass
m3/2( ).
).
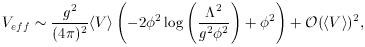
 is the cutoff of the
effective supergravity theory, and
has a minimum around
is the cutoff of the
effective supergravity theory, and
has a minimum around

 0.5
0.5 .
Thus,
.
Thus,  0 ~
MP will be generated and
in this case the subsequent sfermion oscillations will
dominate the energy density and a baryon asymmetry will result
which is independent of inflationary parameters as originally
discussed in
[42,
43]
and will produce nB/s ~ O(1).
Thus we are left with the problem that the baryon asymmetry in
no-scale type models is too large
[55,
53,
56].
0 ~
MP will be generated and
in this case the subsequent sfermion oscillations will
dominate the energy density and a baryon asymmetry will result
which is independent of inflationary parameters as originally
discussed in
[42,
43]
and will produce nB/s ~ O(1).
Thus we are left with the problem that the baryon asymmetry in
no-scale type models is too large
[55,
53,
56].
 2n - 2 /
MP2n - 6 leads to a smaller
initial value for
2n - 2 /
MP2n - 6 leads to a smaller
initial value for  0 and
hence a smaller value for nB/s.
For dimension 6 operators (n = 4), a baryon asymmetry of order
nB/s ~ 10-10 is produced. Finally,
another possible suppression mechanism is to employ the smallness of the
fermion masses. The baryon asymmetry is known to be wiped out if the
net B - L asymmetry vanishes because of the sphaleron
transitions at high temperature. However, Kuzmin, Rubakov and
Shaposhnikov
[58]
pointed out that this erasure can be
partially circumvented if the individual
(B - 3Li) asymmetries,
where i = 1, 2, 3 refers to three generations, do not vanish even when
the total asymmetry vanishes. Even though there is still a tendency
that the baryon asymmetry is erased by the chemical equilibrium due to
the sphaleron transitions, the finite mass of the tau lepton shifts
the chemical equilibrium between B and
L3 towards the B side and leaves a finite
asymmetry in the end. Their estimate is
0 and
hence a smaller value for nB/s.
For dimension 6 operators (n = 4), a baryon asymmetry of order
nB/s ~ 10-10 is produced. Finally,
another possible suppression mechanism is to employ the smallness of the
fermion masses. The baryon asymmetry is known to be wiped out if the
net B - L asymmetry vanishes because of the sphaleron
transitions at high temperature. However, Kuzmin, Rubakov and
Shaposhnikov
[58]
pointed out that this erasure can be
partially circumvented if the individual
(B - 3Li) asymmetries,
where i = 1, 2, 3 refers to three generations, do not vanish even when
the total asymmetry vanishes. Even though there is still a tendency
that the baryon asymmetry is erased by the chemical equilibrium due to
the sphaleron transitions, the finite mass of the tau lepton shifts
the chemical equilibrium between B and
L3 towards the B side and leaves a finite
asymmetry in the end. Their estimate is
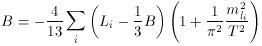
 (T) is
expected to be somewhat smaller than
m
(T) is
expected to be somewhat smaller than
m (0) =
1.777 GeV. Overall, the sphaleron transition suppresses the baryon
asymmetry by a factor of
~ 10-6. This suppression factor is
sufficient to keep the total baryon asymmetry at a reasonable order of
magnitude in many of the cases discussed above.
(0) =
1.777 GeV. Overall, the sphaleron transition suppresses the baryon
asymmetry by a factor of
~ 10-6. This suppression factor is
sufficient to keep the total baryon asymmetry at a reasonable order of
magnitude in many of the cases discussed above.
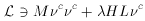
 c -> L +
H*
and
c -> L +
H*
and
 c -> L*
+ H will generate a non-zero
lepton number L
c -> L*
+ H will generate a non-zero
lepton number L  0. The
out-out-equilibrium condition for these decays translates to
10-3
0. The
out-out-equilibrium condition for these decays translates to
10-3  2
MP < M
and M could be as low as O(10) TeV.
(Note that once again in order to
have a non-vanishing contribution to the C and CP violation
in this process at 1-loop, at least 2 flavors of
2
MP < M
and M could be as low as O(10) TeV.
(Note that once again in order to
have a non-vanishing contribution to the C and CP violation
in this process at 1-loop, at least 2 flavors of
 c are required.
For the generation of masses of all three neutrino flavors,
3 flavors of
c are required.
For the generation of masses of all three neutrino flavors,
3 flavors of  c are required.)
Sphaleron effects can transfer this lepton asymmetry into a baryon
asymmetry since now
B - L
c are required.)
Sphaleron effects can transfer this lepton asymmetry into a baryon
asymmetry since now
B - L  0. A
supersymmetric version of this scenario has also been described
[40,
60].
0. A
supersymmetric version of this scenario has also been described
[40,
60].