

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
3.3 Common Big Bang Misconceptions
Although the concept of an isotropically expanding universe is straightforward enough to understand locally, there are a number of conceptual traps lurking in wait for those who try to make global sense of the expansion. The most common sources of error in thinking about the basics of cosmology are discussed below. Some of these may seem rather elementary when written down, but they are all fallacies to be encountered quite commonly in the minds of even the most able students.
THE INITIAL SINGULARITY
THE ORIGIN OF THE REDSHIFT
This would be appropriate in the case of a model
with
(where
THE NATURE OF THE EXPANSION
THE EMPTY UNIVERSE
We therefore start with the normal Minkowski metric,
and consider how this is viewed by a set of fundamental
observers, in the form of particles that are ejected
from r = 0 at t = 0, and which proceed with constant velocity.
The velocity of particles seen at radius r
at time t is therefore a function of radius: v = r /
t (t = H0-1,
as required); particles do not exist beyond the radius
r = ct, at which point they are receding from the origin
at the speed of light. If all clocks are synchronized
at t = 0, then the cosmological time t' is just related to
the background special relativity time via time dilation:
If we also define d
To complete the transition from Minkowski to
fundamental-observer coordinates, we need to eliminate
r. To do this, define the velocity variable
Now, the time-dilation equation gives r in terms of
t and t' as
and the radial increment of proper length is related to
dr via length contraction (since d
The metric therefore becomes
This is the k = -1 Robertson-Walker form, and it demonstrates
several important points. First, since any model with 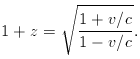
 = 0 (see below), but is
wrong in general. Nevertheless, it is all too common to read
of the latest high-redshift quasar as ``receding at 99.999 . . .
per cent of the speed of light''. The reason the
redshift cannot be interpreted in this way is because
a non-zero mass density must cause gravitational
redshifts [problem 3.4]; even this interpretation is hard
to apply rigorously when redshifts of order unity are attained.
One way of looking at this issue
is to take the rigid point of view that 1 + z tells us
nothing more than how much the universe has expanded
since the emission of the photons we now receive.
Perhaps more illuminating, however, is to realize that,
although the redshift cannot be thought of as a global
Doppler shift, it is correct to think of the effect as
an accumulation of the infinitesimal Doppler
shifts caused by photons passing between fundamental
observers separated by a small distance:
= 0 (see below), but is
wrong in general. Nevertheless, it is all too common to read
of the latest high-redshift quasar as ``receding at 99.999 . . .
per cent of the speed of light''. The reason the
redshift cannot be interpreted in this way is because
a non-zero mass density must cause gravitational
redshifts [problem 3.4]; even this interpretation is hard
to apply rigorously when redshifts of order unity are attained.
One way of looking at this issue
is to take the rigid point of view that 1 + z tells us
nothing more than how much the universe has expanded
since the emission of the photons we now receive.
Perhaps more illuminating, however, is to realize that,
although the redshift cannot be thought of as a global
Doppler shift, it is correct to think of the effect as
an accumulation of the infinitesimal Doppler
shifts caused by photons passing between fundamental
observers separated by a small distance:
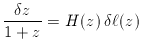

 is a radial increment of proper
distance). This expression may be verified by substitution of the
standard expressions for H (z) and d
is a radial increment of proper
distance). This expression may be verified by substitution of the
standard expressions for H (z) and d / dz.
The nice thing about this way of looking at the result
is that it emphasizes that it is momentum that gets
redshifted; particle
de Broglie wavelengths thus scale with the expansion,
a result that is independent of whether their rest mass is non-zero.
To see this last point, replace d
/ dz.
The nice thing about this way of looking at the result
is that it emphasizes that it is momentum that gets
redshifted; particle
de Broglie wavelengths thus scale with the expansion,
a result that is independent of whether their rest mass is non-zero.
To see this last point, replace d by v dt in general,
and consider the effect of an infinitesimal Lorentz
transformation:
by v dt in general,
and consider the effect of an infinitesimal Lorentz
transformation:  p =
(E / c2)
p =
(E / c2) 
 .
.
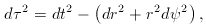
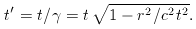
 to be the radial separation between events measured by fundamental observers at
fixed t', the metric can be rewritten as
to be the radial separation between events measured by fundamental observers at
fixed t', the metric can be rewritten as
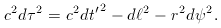
 :
:
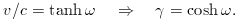
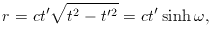
 is at constant t'):
is at constant t'):
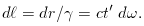
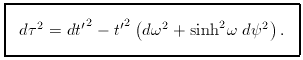
 < 1
will eventually go over to the empty model as R ->
< 1
will eventually go over to the empty model as R ->
 ,
this allows us to demonstrate that the constant of integration
in the Friedmann equation really does correspond to -kc2
(see earlier) in the k = -1 case without using Einstein's field
equations. Second, it shows that it is more useful to
think of the comoving distance Sk (
,
this allows us to demonstrate that the constant of integration
in the Friedmann equation really does correspond to -kc2
(see earlier) in the k = -1 case without using Einstein's field
equations. Second, it shows that it is more useful to
think of the comoving distance Sk ( )
as representing the distance to a galaxy than
)
as representing the distance to a galaxy than  itself. In the empty model, the reason for this is that the
proper length elements dsrc="../GIFS/omega.gif" alt="omega">
become progressively length-contracted at high redshift, giving a
spuriously low value for the distance.
itself. In the empty model, the reason for this is that the
proper length elements dsrc="../GIFS/omega.gif" alt="omega">
become progressively length-contracted at high redshift, giving a
spuriously low value for the distance.