

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
3.4 Observations in Cosmology
The various distances that we have discussed are of course not directly observable; all that we know about a distant object is its redshift. Observers therefore place heavy reliance on formulae for expressing distance in terms of redshift. For high-redshift objects such as quasars, this has led to a history of controversy over whether a component of the redshift could be of non-cosmological origin:
For now, we assume that the cosmological
contribution to the redshift can always be identified.
DISTANCE-REDSHIFT RELATION
For a matter-dominated Friedmann model, this
means that the distance of an object from which we
receive photons today is
Integrals of this form often arise when manipulating Friedmann
models; they can usually be tackled by the substitution
u2 = k (
A more direct derivation could use the parametric solution in
terms of conformal time, plus r =
Although the above is the standard form for Mattig's formula, it is
not always the most computationally convenient, being ill defined
for small
It is often useful in calculations to be able to convert this formula into the
corresponding one for Ck (r). The result is
remembering that R0 = (c / H0)
[(
It is possible to extend this formula to the case of contributions
from pressureless matter (
There is no such compact expression if one
wishes to allow for vacuum energy as well (Dabrowski & Stelmach 1987).
The comoving distance has to be obtained by numerical
integration of the fundamental dr / dz, even in the k = 0 case.
However, for all forms of contribution to the energy
content of the universe, the second-order distance-redshift
relation is identical, and depends only on the deceleration parameter:
[problem 3.4]. The sizes and flux densities of distant objects
therefore determine the geometry of the universe only once an
equation of state is assumed, so that q0 and
CHANGE IN REDSHIFT
(e.g. Lake 1981; Phillipps 1982). The redshift is thus expected
to change by perhaps 1 part in 108 over a human
lifetime. In principle, this sort of accuracy is not
completely out of reach of technology. However, in
practice these cosmological changes will be swamped
if the object changes its peculiar velocity by more
than 3 m s-1 over this period. Since peculiar
velocities of up to 1000 km s-1 are built up
over the Hubble time, the cosmological and intrinsic
redshift changes are clearly of the same order, so that
separating them would be very difficult.
AN OBSERVATIONAL TOOLKIT
so that the comoving volume element is
The proper transverse size of an object seen by us is
its comoving size d
Probably the most important relation for observational cosmology is
that between monochromatic flux density and luminosity.
Start by assuming isotropic emission, so that the photons
emitted by the source pass with a uniform flux density through
any sphere surrounding the source. We can now make a shift of
origin, and consider the RW metric as being centred on the
source; however, because of homogeneity, the comoving distance
between the source and the observer is the same as we would calculate
when we place the origin at our location. The photons from the
source are therefore passing through a sphere, on which we sit,
of proper surface area 4
A word about units: L
The flux density received by a given observer can be expressed
by definition as the product of the specific intensity
I
where B
The form of the above relations lead to the following
definitions for particular kinds of distances:
At least the meaning of the terms is unambiguous enough, which is
not something that can be said for the term effective distance,
sometimes used to denote R0 Sk
(r). Angular-diameter distance versus redshift is illustrated in
figure 3.7.
The last element needed for the analysis of observations
is a relation between redshift and age for the object
being studied. This brings in our earlier relation between
time and comoving radius (consider a null geodesic
traversed by a photon that arrives at the present):
So far, all this is completely general; to complete the toolkit, we need
the crucial input of relativistic dynamics, which is to give the
distance-redshift relation. For almost all observational work, it is usual
to assume the matter-dominated Friedmann models with differential relation
which integrates to
PREDICTING BACKGROUNDS
This may seem a bit of a cheat: we have considered how the
energy density evolves at a point in space, even though we
know that the photons we see today originated at some large
distance. This approach works well enough because of
large-scale homogeneity, but it may be clearer to obtain
the result for the background directly.
Consider a solid angle element d
This volume produces a luminosity V j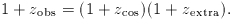
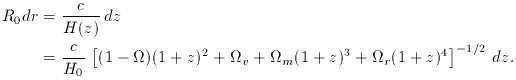
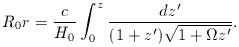
 - 1) / [(
- 1) / [( (1 +
z)].
This substitution produces Mattig's formula (1958),
which is one of the single most useful equations
in cosmology as far as observers are concerned:
(1 +
z)].
This substitution produces Mattig's formula (1958),
which is one of the single most useful equations
in cosmology as far as observers are concerned:
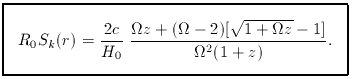
 now -
now -  emit.
The generalisation of the sine rule is required in this method:
Sk (a - b) = Sk (a) Ck
(b) - Ck (a) Sk (b).
emit.
The generalisation of the sine rule is required in this method:
Sk (a - b) = Sk (a) Ck
(b) - Ck (a) Sk (b).
 . A better version of
the relation for low-density universes is
. A better version of
the relation for low-density universes is
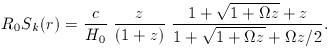
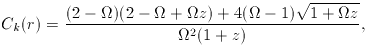
 - 1) / k]-1/2.
- 1) / k]-1/2.
 m) and radiation (
m) and radiation ( r):
r):
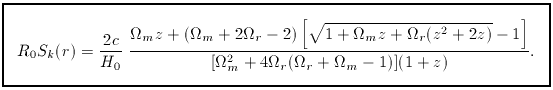
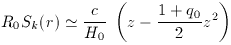
 0 can be related.
0 can be related.
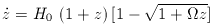
 .
We write the metric in the form
.
We write the metric in the form
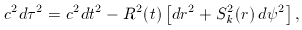
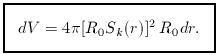
 Sk (r) times the scale factor
at the time of emission:
Sk (r) times the scale factor
at the time of emission:
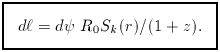
 [R0 Sk (r)]2. But redshift
still affects the flux density in four further ways: photon energies
and arrival rates are redshifted, reducing the flux density
by a factor (1 + z)2; opposing this, the bandwidth
d
[R0 Sk (r)]2. But redshift
still affects the flux density in four further ways: photon energies
and arrival rates are redshifted, reducing the flux density
by a factor (1 + z)2; opposing this, the bandwidth
d  is
reduced by a factor 1 + z, so the energy flux per unit bandwidth
goes down by one power of 1 + z; finally, the observed photons
at frequency
is
reduced by a factor 1 + z, so the energy flux per unit bandwidth
goes down by one power of 1 + z; finally, the observed photons
at frequency  0 were
emitted at frequency
0 were
emitted at frequency  0 (1
+ z), so
the flux density is the luminosity at this frequency, divided
by the total area, divided by 1 + z:
0 (1
+ z), so
the flux density is the luminosity at this frequency, divided
by the total area, divided by 1 + z:
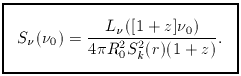
 in this equation would be measured
in units of W Hz-1. Recognizing that emission is
often not isotropic, it is common to consider instead the
luminosity emitted into unit solid angle - in which case there
would be no factor of 4
in this equation would be measured
in units of W Hz-1. Recognizing that emission is
often not isotropic, it is common to consider instead the
luminosity emitted into unit solid angle - in which case there
would be no factor of 4 , and the
units of L
, and the
units of L would be
W Hz-1 sr-1.
would be
W Hz-1 sr-1.
 (the flux density
received from unit solid angle of the sky) and the solid
angle subtended by the source: S
(the flux density
received from unit solid angle of the sky) and the solid
angle subtended by the source: S = I
= I d
d  .
Combining the angular size and flux-density
relations thus gives the relativistic version
of surface-brightness conservation. This is independent
of cosmology (and a more general derivation is given in chapter 4):
.
Combining the angular size and flux-density
relations thus gives the relativistic version
of surface-brightness conservation. This is independent
of cosmology (and a more general derivation is given in chapter 4):
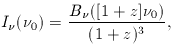
 is
surface brightness (luminosity
emitted into unit solid angle per unit area of source).
We can integrate over
is
surface brightness (luminosity
emitted into unit solid angle per unit area of source).
We can integrate over  0 to
obtain the corresponding total or bolometric formulae, which are
needed e.g. for spectral-line emission:
0 to
obtain the corresponding total or bolometric formulae, which are
needed e.g. for spectral-line emission:
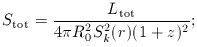
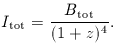

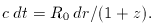
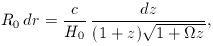
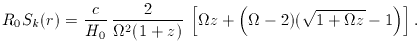
 for some process as a function of frequency and epoch,
and want to predict the current background seen at frequency
for some process as a function of frequency and epoch,
and want to predict the current background seen at frequency  0.
The total spectral energy density created during time dt is
j
0.
The total spectral energy density created during time dt is
j (
( 0[1 + z], z)
dt; this reaches the present reduced by the volume expansion
factor (1 + z)-3.
The redshifting of frequency does not matter:
0[1 + z], z)
dt; this reaches the present reduced by the volume expansion
factor (1 + z)-3.
The redshifting of frequency does not matter:  scales as 1 + z, but so does d
scales as 1 + z, but so does d  . The reduction in energy density
caused by lowering photon energies is then exactly compensated
by a reduced bandwidth, leaving the spectral energy density
altered only by the change in proper photon number density.
Inserting the redshift-time relation, and multiplying by c /
4
. The reduction in energy density
caused by lowering photon energies is then exactly compensated
by a reduced bandwidth, leaving the spectral energy density
altered only by the change in proper photon number density.
Inserting the redshift-time relation, and multiplying by c /
4 to obtain the specific intensity, we get
to obtain the specific intensity, we get
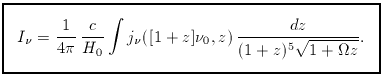
 : at redshift z,
this area on the sky for some radial increment dr defines
a proper volume
: at redshift z,
this area on the sky for some radial increment dr defines
a proper volume

 , from which we
can calculate the observed flux density S
, from which we
can calculate the observed flux density S = L
= L / [4
/ [4 (R0 Sk)2 (1 +
z)]. Since surface brightness is just flux density per unity
solid angle, this gives
(R0 Sk)2 (1 +
z)]. Since surface brightness is just flux density per unity
solid angle, this gives