

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
3.5 The Anthropic Principle
Our discussion of cosmology so far has leaned heavily on the Copernican principle that we are not privileged observers of the universe. However, there are some aspects of the subject for which this principle has to be discarded; as in quantum mechanics, we have to ask whether the mere presence of an observer influences the system under study. At first sight, it may seem absurd to think of humanity influencing in any way the global properties of the universe, but the simple fact of our existence does turn out to have profound consequences. These ideas are given the label ``anthropic'', and we speak of the anthropic principle when discussing the universe in the context of the existence of observers. However, this is an area that generates controversy, and not everyone will agree on the degree of importance of anthropic ideas. See Barrow & Tipler (1986) for a thorough review of the subject. Like religious schisms, the anthropic dogma comes in varying forms and degrees of elaboration. We can distinguish perhaps three sets of attitudes to anthropic reasoning: trivial, weak and strong anthropic principles.
THE TRIVIAL ANTHROPIC PRINCIPLE
However, anthropic arguments of this type have an honourable history
from the 19th century, when the Earth could not
be dated directly. At that time, Lord Kelvin was
advocating an age for the Earth of only ~ 107
years, based on its cooling time. Evolutionary
biologists were able to argue that this was an
inadequate time to allow the development of species,
a conclusion that was vindicated by the discovery
of radioactivity (which allowed both the dating of the
Earth and showed the flaw in Kelvin's argument).
Here was an excellent example of
important astronomical conclusions being drawn from
observations of life on Earth.
THE WEAK ANTHROPIC PRINCIPLE
The most striking of Dicke's arguments is based
upon the mechanism for the production of the elements. As we shall see,
it is now thought virtually certain that the abundances of the
light elements up to 7Li were determined by the
progress of nuclear reactions in the early stages of
the big bang. Heavier elements were produced at a much later stage by
fusion in stars. Incidentally, this division of
labour represents an ironic end to a historically
important debate concerning the origin of the universe,
which dominated cosmology in the 1960s. The epochal
paper that became universally known just
as B2FH (Burbidge, Burbidge, Fowler & Hoyle
1957) was concerned with showing how the elements could
be built up by nuclear reactions in stars.
Although this was not the motivation for the work, these
mechanisms provided a vital defence for the
steady-state model (which never passes through a hot phase)
against the belief of Gamow and coworkers that all
elements could be synthesized in the big bang
(Gamow 1946; Alpher, Bethe & Gamow 1948).
Although the steady-state model passed away, the
arguments of B2FH have become part of current
orthodoxy, leaving only the lightest elements adhering to Gamow's vision.
Now, the fascinating aspect of all this is that
synthesis of the higher elements is rather hard,
owing to the non-existence of stable elements
with atomic weights A = 5 or A = 8. This makes it hard to
build up heavy nuclei by collisions of 1H, 2D,
3He and 4He nuclei. The only reason that
heavier elements are produced at all is the reaction
A three-body process like this will only proceed at a
reasonable rate if the cross-section for the process
is resonant: i.e. if there is an excited
energy level of the carbon nucleus that matches
the typical energy of three alpha particles in a stellar
interior. The lack of such a level would lead to negligible
production of heavy elements - and no carbon-based life.
Using these arguments, Hoyle made a breathtaking leap of
the imagination to predict that carbon would display such
a resonance, which was duly found to be the case (Hoyle et al. 1953).
In a sense, this is just trivial anthropic reasoning:
we see carbon on Earth, and nuclear physics gives us
an inevitable conclusion to draw. And yet, one is struck
by the coincidence: if the energy levels of
carbon had been only slightly different, then it is
reasonable to assume that the development of
life anywhere in the universe would never have occurred.
Does this mean that some controlling agent designed
nuclear physics specifically to produce life? Perhaps, but it
is not so easy to prove one way or the other, as we can see from the
following arguments.
Suppose we imagine some process that produces an
ensemble of a large number of universes
with widely varying properties or even physical laws.
What the weak anthropic principle points out is that
only those members of the ensemble that are
constructed so as to admit the production of intelligent
life at some stage in their evolution will ever
be the subject of cosmological enquiry.
The fact that we are observers means that, if the
production of life is at all a rare event, any universe that
we can see is virtually guaranteed to display
bizarre and apparently improbable coincidences.
The 12C energy level is one such; another goes under the
heading of Dirac's large-number hypothesis.
Dirac noted that very large dimensionless numbers
often arise in both particle physics and cosmology.
The ratio of the electrostatic and gravitational forces
experienced by an electron in a hydrogen atom is
one of the problems of unifying gravity and other forces
is understanding how such a vast dimensionless number
can be generated naturally. In a cosmological context,
the weakness of gravity manifests itself in the fact that
the Hubble radius is enormously greater than the Planck length:
This number is very nearly the 1.5 power of the previous
large number: it is as if these large numbers were quantized
in steps of 1020. Dirac proposed that the coincidence
must indicate a causal relation; requiring the proportionality to
hold at all times then yields the radical consequence
(because H0 declines as ~ t-1 as the
universe ages).
Geological evidence shows
that this prediction is not upheld in practice, since
the sun would have been hotter in the past.
A less radical explanation of the large-number coincidence
uses the anthropic idea that life presumably requires the
existence of elements other than hydrogen and helium.
The universe must therefore be old enough to allow typical
stars to go through their life cycle and produce ``metals''.
This condition can be expressed in terms of fundamental
constants as follows. Stars have masses of the order of
the Chandrasekhar mass
where mp is the proton mass (see chapter 2).
The luminosity of a star dominated by electron-scattering opacity is
[problem 5.1]
The characteristic lifetime of a star, MChandra
c2 / L,
can thus also be expressed in fundamental constants, and is
Comparing with the above,
we see that the large-number coincidence is just
t* ~ H0-1; i.e. the
universe must be old enough for the stars to age. The fact that the
universe is not very much older than this may tell us that
we are privileged to be in the first generation of
intelligence to arise after the big bang: civilizations
arising in >> 1010 years time will probably not spend
their time in cosmological enquiry, as they will be in contact
with experienced older races who know the answers already.
Lastly, the coincidence can be used to argue for the fundamental
correctness of the big bang as against competitors such as the steady-state
theory; if the universe is in reality very much older than
t*, there is no explanation for the coincidence
between t* and H0-1.
In short, the weak anthropic principle states
that, because intelligent life is necessary for cosmological
enquiry to take place, this already imposes strong
selection effects on cosmological observations.
Note that, despite the name, there is no requirement for
the life to be human, or even carbon based. All we
say is that certain conditions can be ruled out if they
do not lead to observers, and this is one of the weaknesses
of the principle: are we really sure that life based on
elements less massive than carbon is impossible?
The whole point of these arguments is that it only has to happen once.
It is nevertheless at least plausible that the ``anthropic''
term may not be a complete misnomer. It has been argued (see
Carter 1983) that intelligent life is intrinsically an extremely
unlikely phenomenon, where the mean time for development could be very long:
If the inequality was sufficiently great, it would be surprising to
find even one intelligent system within the current horizon. The
anthropic principle provides a means for understanding why the
number is non-zero, even when the expectation is small, but
there would be no reason to expect a second system; humanity
would then probably be alone in the universe.
On the other hand,
OTHER WEAK ANTHROPIC DEDUCTIONS
A first coincidence to consider is that recombination and
matter-radiation equality occur at relatively similar times;
why is this? Recombination requires a temperature of
roughly the ionization potential of hydrogen:
The mass ratio of baryons and photons at recombination
is therefore 1372 mp / me ~
107.5, and the universe
will be matter dominated at recombination unless the
ratio of photon and proton number densities exceeds this value.
At high temperatures, kT > mp c2,
baryon, antibaryon and photon
numbers will be comparable; it is thought that the present
situation arises from a particle-physics asymmetry between
matter and antimatter, so that baryons and
antibaryons do not annihilate perfectly (see chapter 9).
Matter-radiation equality thus arises anywhere after
a redshift 107.5 times larger than that of last
scattering, and could be infinitely delayed if the
matter/antimatter asymmetry were small enough.
The approximate coincidence in epochs says that the size of the
particle/antiparticle asymmetry is indeed roughly
1372 mp / me, and it is not
implausible that such
a relation might arise from a complete particle physics
model. At any rate, it seems to have no bearing on anthropic issues.
The anthropic argument for the age of the universe
lets us work out the time of recombination, if we accept
for the moment that
Finally, what do anthropic arguments have to say about the cosmic
density parameter,
so that
These arguments are impressive, but frustratingly
limited. Although a rough allowed area of parameter space
can be delineated, proper physical mechanisms are
required to explain why a particular point in the
parameter space was selected by reality.
Given such a mechanism, why do we need anthropic reasoning
at all? Worse still, anthropic reasoning tends to predict a
universe at the extremes of the allowed range. Consider a
generator of an ensemble of universes creating them with
various values of
THE STRONG ANTHROPIC PRINCIPLE
PROBLEMS
(3.1)
Show that the Robertson-Walker metric satisfies Einstein's
equations and obtain the Friedmann equation(s).
(3.2)
An object is observed at redshift z in a Friedmann universe
with density parameter
(3.3)
An object at comoving radius r is observed at two periods
six months apart, allowing the parallax angle
(3.4)
Consider the second-order corrections to the relation
between redshift and angular-diameter distance [c /
H0] D(z):
to second order. Attempt to account for this relation with a Newtonian
analysis.
(3.6)
The steady-state universe has R  1 Gyr old merely by
noting that carbon-based life has formed, and that there needed to be time
for typical stars to go through their life cycle
and distribute heavy elements in order for this to
have happened. The existence of humanity thus
gives us a bound on H0. That is about as far as
such trivial anthropic arguments go in cosmology;
they are in a sense unnecessary, as we have direct
dating of the Earth to set a much more precise
limit on H0, a constraint that was astronomically
important in the early days of the distance scale,
when values of H0
1 Gyr old merely by
noting that carbon-based life has formed, and that there needed to be time
for typical stars to go through their life cycle
and distribute heavy elements in order for this to
have happened. The existence of humanity thus
gives us a bound on H0. That is about as far as
such trivial anthropic arguments go in cosmology;
they are in a sense unnecessary, as we have direct
dating of the Earth to set a much more precise
limit on H0, a constraint that was astronomically
important in the early days of the distance scale,
when values of H0  500 km s-1 were suggested.
500 km s-1 were suggested.
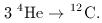
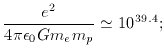
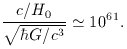
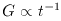
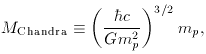
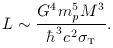
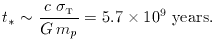
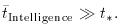
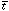 Intelligence may be shorter,
and then other intelligences would be common. Either possibility
is equally consistent with the selection effect imposed by our existence,
although the fact that life on Earth took billions of years to
develop is consistent with the former view; if life is a rare
event, it would not appear early in the allowed span of time.
Intelligence may be shorter,
and then other intelligences would be common. Either possibility
is equally consistent with the selection effect imposed by our existence,
although the fact that life on Earth took billions of years to
develop is consistent with the former view; if life is a rare
event, it would not appear early in the allowed span of time.
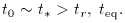
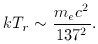
 ~ 1 (see below).
The age for an Einstein-de Sitter model would tell us
both H0 &
~ 1 (see below).
The age for an Einstein-de Sitter model would tell us
both H0 &  0, and
hence the current number density of photons, if we
could obtain the photon-to-baryon ratio from
fundamental arguments. Since n
0, and
hence the current number density of photons, if we
could obtain the photon-to-baryon ratio from
fundamental arguments. Since n
 T
T 3,
that would give the present photon temperature, and hence
the redshift of recombination. The fact that this was
relatively recent (only at z ~ 103 reflects the
fact that the photon-to-baryon ratio is ~ 107
rather than a much larger number.
3,
that would give the present photon temperature, and hence
the redshift of recombination. The fact that this was
relatively recent (only at z ~ 103 reflects the
fact that the photon-to-baryon ratio is ~ 107
rather than a much larger number.
 ?
We have already mentioned the instability in
?
We have already mentioned the instability in  :
:
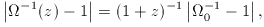
 (z) has to be
fine-tuned at early epochs
to achieve
(z) has to be
fine-tuned at early epochs
to achieve 
 1 now. We can go some way
towards explaining this by appealing to some results
that will be proved in later chapters. The formation of
galaxies can only occur at a redshift zf such that
1 now. We can go some way
towards explaining this by appealing to some results
that will be proved in later chapters. The formation of
galaxies can only occur at a redshift zf such that
 (zf) ~ 1,
otherwise growth of density perturbations switches off;
(zf) ~ 1,
otherwise growth of density perturbations switches off;
 0 must be unity to
within a factor ~ (1 + zf).
The redshift zf must occur after matter-radiation
equality, otherwise radiation pressure would prevent
galaxy-scale systems from collapsing. Any universe with
0 must be unity to
within a factor ~ (1 + zf).
The redshift zf must occur after matter-radiation
equality, otherwise radiation pressure would prevent
galaxy-scale systems from collapsing. Any universe with
 >> 10-3 at t
= t* would then have
great difficulty in generating the nonlinear systems needed for life.
Similar arguments can be made concerning the contribution
of a cosmological constant to
>> 10-3 at t
= t* would then have
great difficulty in generating the nonlinear systems needed for life.
Similar arguments can be made concerning the contribution
of a cosmological constant to  (Weinberg 1989; Efstathiou 1995):
structures cannot form after the time at which the universe
becomes dominated by any cosmological term.
On the other hand, because formation is constrained to occur
between a redshift of order unity and 103, the vacuum
density could presently exceed the density in matter
by a factor of up to 109 without
preventing structure formation. There is no anthropic
reason for it to be any smaller.
(Weinberg 1989; Efstathiou 1995):
structures cannot form after the time at which the universe
becomes dominated by any cosmological term.
On the other hand, because formation is constrained to occur
between a redshift of order unity and 103, the vacuum
density could presently exceed the density in matter
by a factor of up to 109 without
preventing structure formation. There is no anthropic
reason for it to be any smaller.
 (t*). Owing to the fine-tuning
required, we expect that the probability of a given result
is a strongly increasing function of |
(t*). Owing to the fine-tuning
required, we expect that the probability of a given result
is a strongly increasing function of | - 1|. Multiply
this by a probability of generating intelligence that
declines with |
- 1|. Multiply
this by a probability of generating intelligence that
declines with | - 1| slowly at
first, and we should expect
a life-selected universe to have a peak probability near to the
very largest or smallest possible values of |
- 1| slowly at
first, and we should expect
a life-selected universe to have a peak probability near to the
very largest or smallest possible values of | - 1|.
This is not the observed situation: anthropic arguments
may therefore not be relevant to
determining
- 1|.
This is not the observed situation: anthropic arguments
may therefore not be relevant to
determining  , even if their
importance in explaining the large-number ratios cannot be challenged.
, even if their
importance in explaining the large-number ratios cannot be challenged.
 . Calculate the observed rate of change of
redshift for the object. What fractional precision in observed
frequency would be needed to detect cosmological deceleration
in a decade?
. Calculate the observed rate of change of
redshift for the object. What fractional precision in observed
frequency would be needed to detect cosmological deceleration
in a decade?
 to be
observed for a baseline of D perpendicular to the line
of sight. Show that the parallax distance D /
to be
observed for a baseline of D perpendicular to the line
of sight. Show that the parallax distance D /  is R0 Sk (r) / Ck
(r) and give an expression for this valid to second order in redshift.
is R0 Sk (r) / Ck
(r) and give an expression for this valid to second order in redshift.
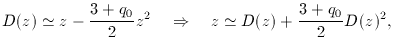
 eHt,
zero curvature of its comoving coordinates (k = 0),
and a proper density of all objects that is constant
in time. Show that the comoving volume out to redshift z
is V (z) = 4
eHt,
zero curvature of its comoving coordinates (k = 0),
and a proper density of all objects that is constant
in time. Show that the comoving volume out to redshift z
is V (z) = 4  (cz /
H)3 / 3, and hence that the number-count
slope for objects at typical redshift z becomes
(cz /
H)3 / 3, and hence that the number-count
slope for objects at typical redshift z becomes
 = [(3 +
= [(3 +  ) ln z]-1 for
z >> 1, where
) ln z]-1 for
z >> 1, where  is the
spectral index of the objects.
is the
spectral index of the objects.