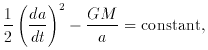
where
and a (t) is the expansion factor (such that the distance between
conserved objects scales with the expansion of the universe as
a (t)). The mass density
The baryon density is an adjustable parameter in this theory. It is
impressive that the value of
We have a check on
The straightforward reading of the SNeIa z-m relation within the
Friedmann-Lemaître model is that
Our tour of the second set of tests in
Table 1, that probe space-time
geometry, shows no postulates that appear artificial, which is
encouraging. But we do see that each constraint is met with a new free
parameter, which is a dangerous operation, to quote
de Sitter (1931).
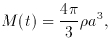
 (t) includes rest mass and the mass
equivalent of energy; equation (1) is a relativistic
expression. But since you can guess at its form by analogy to Newtonian
mechanics it is not a very deep application of general relativity
theory. For that we must consider more of the cosmological tests.
(t) includes rest mass and the mass
equivalent of energy; equation (1) is a relativistic
expression. But since you can guess at its form by analogy to Newtonian
mechanics it is not a very deep application of general relativity
theory. For that we must consider more of the cosmological tests.
 baryon that yields a
satisfactory fit to the the observed abundances of the light element
fits the astronomical surveys of the baryon density
(Fukugita et
al. 1998),
but the check is only good to a factor of three or
so. The wanted baryon density is less than the mass density parameter
baryon that yields a
satisfactory fit to the the observed abundances of the light element
fits the astronomical surveys of the baryon density
(Fukugita et
al. 1998),
but the check is only good to a factor of three or
so. The wanted baryon density is less than the mass density parameter
 m indicated
by dynamical studies of the motions of galaxies
relative to the general expansion (as discussed in
Section 3.1). That is
remedied by an hypothesis, that the mass of the universe is dominated by
nonbaryonic matter. The straightforward reading of the dynamical
estimates is that
m indicated
by dynamical studies of the motions of galaxies
relative to the general expansion (as discussed in
Section 3.1). That is
remedied by an hypothesis, that the mass of the universe is dominated by
nonbaryonic matter. The straightforward reading of the dynamical
estimates is that  m is less than unity, contrary to the simple
Einstein-de Sitter case. A popular remedy is another postulate, that the
mass of the universe is dominated by dark matter outside the
concentrations of galaxies.
m is less than unity, contrary to the simple
Einstein-de Sitter case. A popular remedy is another postulate, that the
mass of the universe is dominated by dark matter outside the
concentrations of galaxies.
 m, from the magnificent work by two groups
(Perlmutter et
al. 1998a,
b;
Reiss et al. 1998)
on the
curvature of the redshift-magnitude (z-m) relation for supernovae of
type Ia. A cautionary note is in order, however. The most distant
supernovae are fainter than would be expected in the Einstein-de Sitter
case. How do we know that is not because the more distant supernovae are
less luminous? The authors present careful checks, but the case has to
be indirect: no one is going to examine any of these
supernovae up close, let alone make the trip back in time to compare
distant supernovae to nearer examples. In short, the
supernovae measurement is a great advance, beautifully and
carefully done, but it does not come with a guarantee. The point is
obvious to astronomers but not always to their colleagues in physics,
and so might well be encoded in the Tantalus Principle: in astronomy you
can look but never touch (with a few exceptions, such as objects in the
Solar System, that are quite irrelevant for our purpose).
m, from the magnificent work by two groups
(Perlmutter et
al. 1998a,
b;
Reiss et al. 1998)
on the
curvature of the redshift-magnitude (z-m) relation for supernovae of
type Ia. A cautionary note is in order, however. The most distant
supernovae are fainter than would be expected in the Einstein-de Sitter
case. How do we know that is not because the more distant supernovae are
less luminous? The authors present careful checks, but the case has to
be indirect: no one is going to examine any of these
supernovae up close, let alone make the trip back in time to compare
distant supernovae to nearer examples. In short, the
supernovae measurement is a great advance, beautifully and
carefully done, but it does not come with a guarantee. The point is
obvious to astronomers but not always to their colleagues in physics,
and so might well be encoded in the Tantalus Principle: in astronomy you
can look but never touch (with a few exceptions, such as objects in the
Solar System, that are quite irrelevant for our purpose).
 m is well below unity, consistent with dynamics,
and that there is a significant contribution to the stress-energy tensor
from Einstein's cosmological constant
m is well below unity, consistent with dynamics,
and that there is a significant contribution to the stress-energy tensor
from Einstein's cosmological constant  (or a term in the
stress-energy tensor that acts like
(or a term in the
stress-energy tensor that acts like  ). The latter has to be
counted as another hypothesis, of course. This in turn can be checked by
still more cosmological tests, such as the expansion time. But as
discussed in the next section we don't yet have the wanted precision.
). The latter has to be
counted as another hypothesis, of course. This in turn can be checked by
still more cosmological tests, such as the expansion time. But as
discussed in the next section we don't yet have the wanted precision.


