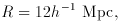
where Hubble's constant is written as
and the dimensionless parameter is thought to be in
the range 0.5
The divergence is with respect to comoving coordinates x,
where a physical length interval is
Here n is the unit normal of the sphere,
The power law is a good approximation if
For a sphere centered on the Virgo Cluster, with us on the
surface, estimates of the mean radial flow through the sphere
and the contrast
The velocity is from a survey in progress
by Tonry et
al. (1998);
it is consistent with earlier measurements (eg.
Faber & Burstein
1988).
The density contrast in counts of IRAS galaxies within
our distance from the Virgo cluster is
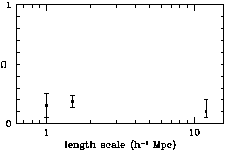
This is plotted as the right-hand point in
Figure 1.
There are three key assumptions. First, the analysis uses
conventional gravity physics. An alternative,
Milgrom's (1995)
modified Newtonian dynamics (MOND), has been quite durable in
applications to individual galaxies
(de Blok & McGaugh
1998).
An extension to the analysis of large-scale flows would be
interesting, but the focus here is the test of cosmology based on
the conventional gravity physics of general relativity
theory. Second, the relation between peculiar velocities and the
mass distribution follows from the assumption that structure
grew by gravity out of small primeval departures from
homogeneity. (Thus the boundary condition for
eq. [7] is D (t) -> 0 at
z >> 1.) Most dynamical measures of
If
The theory of the origin of the light elements requires baryon
density parameter 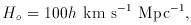
 h
h
 0.8. In the
Friedmann-Lemaître model the gravitational
attraction of the mass excess in this region
produces a peculiar motion of inflow (relative to the general
expansion of the universe). In linear perturbation theory the
mass conservation law relates the peculiar velocity
0.8. In the
Friedmann-Lemaître model the gravitational
attraction of the mass excess in this region
produces a peculiar motion of inflow (relative to the general
expansion of the universe). In linear perturbation theory the
mass conservation law relates the peculiar velocity 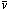 (
(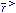 , t) and the mass density contrast
, t) and the mass density contrast
 (
(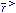 , t) =
, t) = 
 /
/  by the equation
by the equation
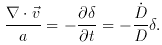
 r = a (t)
r = a (t) x (and the expansion
parameter a (t) appears in eq. [1]). The density fluctuations are
assumed to have grown by gravity out of small primeval irregularities,
so the mass density contrast varies as
x (and the expansion
parameter a (t) appears in eq. [1]). The density fluctuations are
assumed to have grown by gravity out of small primeval irregularities,
so the mass density contrast varies as 
 D (t), where
D (t) is the growing solution to the time evolution of
D (t), where
D (t) is the growing solution to the time evolution of  in
linear perturbation theory. The result of integrating
equation (5) over a sphere of radius R and applying
Gauss's theorem is the wanted relation,
in
linear perturbation theory. The result of integrating
equation (5) over a sphere of radius R and applying
Gauss's theorem is the wanted relation,
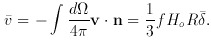
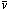 is
the radial inward peculiar velocity averaged over the surface,
and
is
the radial inward peculiar velocity averaged over the surface,
and 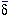 =
=  M/M
is the mass contrast
averaged within the sphere. The dimensionless factor f is
M/M
is the mass contrast
averaged within the sphere. The dimensionless factor f is
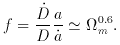
 = 0 or space
curvature vanishes.
= 0 or space
curvature vanishes.
 g =
g =  M/M in galaxy counts within the sphere are
M/M in galaxy counts within the sphere are
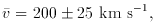
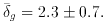
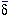 = 1.4
(Strauss et al. 1992).
IRAS galaxies are detected because they are
rich in gas and have high star formation rates, making them
prominent in the 60 to 100 micron range of the IRAS satellite
survey. IRAS galaxies avoid dense regions, likely because
collisions and the ram pressure of intracluster gas have stripped
the galaxies of the gas that fuels bursts of star
formation and high infrared luminosity; a
commonly used correction factor of 1.4 would bring the contrast
for optical galaxy counts to
= 1.4
(Strauss et al. 1992).
IRAS galaxies are detected because they are
rich in gas and have high star formation rates, making them
prominent in the 60 to 100 micron range of the IRAS satellite
survey. IRAS galaxies avoid dense regions, likely because
collisions and the ram pressure of intracluster gas have stripped
the galaxies of the gas that fuels bursts of star
formation and high infrared luminosity; a
commonly used correction factor of 1.4 would bring the contrast
for optical galaxy counts to  g = 2. A
preliminary analysis of the Optical Redshift Survey
(Santiago et
al. 1996)
by Strauss (1998)
gives
g = 2. A
preliminary analysis of the Optical Redshift Survey
(Santiago et
al. 1996)
by Strauss (1998)
gives  g ~ 3.
With
g ~ 3.
With 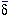 =
= 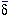 g,
equations (6) to (8) give
g,
equations (6) to (8) give
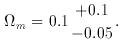
 m use this
assumption; the exception is relaxed systems that have forgotten
their initial conditions (as in the velocity dispersion measure used by
Marzke et al. 1995.)
We have no viable alternative to the gravitational
instability picture for structure formation on large scales, but
it will be checked by consistency with all the other
cosmological tests, when they are better established. Third, and most
contentious, equation (9) assumes the mass
clusters with the galaxies. If the mass contrast were reduced to
m use this
assumption; the exception is relaxed systems that have forgotten
their initial conditions (as in the velocity dispersion measure used by
Marzke et al. 1995.)
We have no viable alternative to the gravitational
instability picture for structure formation on large scales, but
it will be checked by consistency with all the other
cosmological tests, when they are better established. Third, and most
contentious, equation (9) assumes the mass
clusters with the galaxies. If the mass contrast were reduced to
 ~ 0.2
~ 0.2  g then the other
numbers would
be consistent with
g then the other
numbers would
be consistent with  m = 1. The concept that the galaxy
distribution may be a biased measure of the mass distribution
has been influential, and rightly so; this important issue had to
be explored. But as discussed next I think it is also fair to say that
there never was any evidence for what I would expect to be the
distinctive signature of biasing: void galaxies.
m = 1. The concept that the galaxy
distribution may be a biased measure of the mass distribution
has been influential, and rightly so; this important issue had to
be explored. But as discussed next I think it is also fair to say that
there never was any evidence for what I would expect to be the
distinctive signature of biasing: void galaxies.
 m = 1 we
must decide where most of the mass is. It can't be
in groups and clusters of galaxies:
Figure 1 shows that analyses
similar to the above yield similar values of
m = 1 we
must decide where most of the mass is. It can't be
in groups and clusters of galaxies:
Figure 1 shows that analyses
similar to the above yield similar values of  m in the Local Group
(Peebles 1996)
and in clusters of galaxies
(Carlberg et al. 1996).
That leaves the voids, spaces
between the concentrations of giant galaxies. We
know the voids are not undisturbed: absorption lines in
quasar spectra show that at redshift z = 3 space was filled with
clouds of hydrogen. Thus voids would
have to be regions where star or galaxy formation was suppressed.
I find it hard to believe the suppression was so complete as to
leave nothing observable; surely there would be irregulars or
dwarfs from almost failed seeds. Searches in relatively nearby
voids, where galaxies are observable well into the faint end of
the luminosity function, reveal no such population. Perhaps the
gravitational growth of clustering swept the void galaxies into
the concentrations of normal ones, but in that case gravity would
have pulled the mass with the galaxies, suppressing biasing
(Tegmark & Peebles
1998).
Perhaps our picture for structure
formation needs tuning; that will be checked as the
cosmological tests improve. The straightforward reading is that biasing
is not a strong factor;
m in the Local Group
(Peebles 1996)
and in clusters of galaxies
(Carlberg et al. 1996).
That leaves the voids, spaces
between the concentrations of giant galaxies. We
know the voids are not undisturbed: absorption lines in
quasar spectra show that at redshift z = 3 space was filled with
clouds of hydrogen. Thus voids would
have to be regions where star or galaxy formation was suppressed.
I find it hard to believe the suppression was so complete as to
leave nothing observable; surely there would be irregulars or
dwarfs from almost failed seeds. Searches in relatively nearby
voids, where galaxies are observable well into the faint end of
the luminosity function, reveal no such population. Perhaps the
gravitational growth of clustering swept the void galaxies into
the concentrations of normal ones, but in that case gravity would
have pulled the mass with the galaxies, suppressing biasing
(Tegmark & Peebles
1998).
Perhaps our picture for structure
formation needs tuning; that will be checked as the
cosmological tests improve. The straightforward reading is that biasing
is not a strong factor;  m
is substantially less than unity. This is the basis for the grades
in line 1a in Table 2. The grades
are subject to negotiation, of
course; the discovery of a population of void galaxies would
make a big difference to me.
m
is substantially less than unity. This is the basis for the grades
in line 1a in Table 2. The grades
are subject to negotiation, of
course; the discovery of a population of void galaxies would
make a big difference to me.
 baryon = 0.02 / h2 ~ 0.04 for
h = 0.7. It is not easy to reconcile the dynamical analyses
with such a small value for
baryon = 0.02 / h2 ~ 0.04 for
h = 0.7. It is not easy to reconcile the dynamical analyses
with such a small value for  m. As I noted in the last section,
the common assumption is that the mass of the universe is dominated by
nonbaryonic dark matter. There certainly is
nothing unreasonable about the idea---Nature need not have
put most of the matter in a readily observable form---but the
cosmology certainly would be cleaner if we had a laboratory detection of
this hypothetical mass component.
m. As I noted in the last section,
the common assumption is that the mass of the universe is dominated by
nonbaryonic dark matter. There certainly is
nothing unreasonable about the idea---Nature need not have
put most of the matter in a readily observable form---but the
cosmology certainly would be cleaner if we had a laboratory detection of
this hypothetical mass component.