


3.2. Expansion Rate and Time
Since we are considering what the Friedmann-Lemaître model does and
does not predict we should note that the model allows solutions without
a Big Bang, that trace back through a bounce to contraction from
arbitrarily low density. This requires  > 0 and positive
space curvature, and, if the universe is going to contract by a
substantial factor before bouncing, very large space curvature and small
matter density: the redshift at
the bounce is zmax ~ |
> 0 and positive
space curvature, and, if the universe is going to contract by a
substantial factor before bouncing, very large space curvature and small
matter density: the redshift at
the bounce is zmax ~ | R| /
R| /  m.
The bounce case is seldom mentioned, and I suspect rightly so, for
apart from the bizarre initial conditions the redshift
zmax required for light element production requires
quite unacceptable density parameters. If this assessment is
valid we are left with Friedmann-Lemaître solutions that trace back to
infinite density, which is bizarre enough but maybe can be
finessed by inflation and resolved by better gravity physics.
m.
The bounce case is seldom mentioned, and I suspect rightly so, for
apart from the bizarre initial conditions the redshift
zmax required for light element production requires
quite unacceptable density parameters. If this assessment is
valid we are left with Friedmann-Lemaître solutions that trace back to
infinite density, which is bizarre enough but maybe can be
finessed by inflation and resolved by better gravity physics.
A Friedmann-Lemaître model that expands from exceedingly high
density predicts that
stellar evolution ages and radioactive decay ages are less than
the cosmological expansion time t0. Numerical examples are
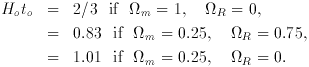 (10)
(10)
The Hubble Space
Telescope Key Project
(Freedman et al. 1998;
Madore et
al. 1998) reports
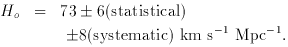 (11)
(11)
The systematic error includes length scale calibrations common to
most measurements of H0. A recent survey of evolution ages of
the oldest globular cluster stars yields 11.5 ± 1.3 Gyr.
(Chaboyer et al. 1998).
We have to add the time for expansion from very high
redshift to the onset of star formation; a commonly used nominal
value is 1 Gyr. If the universe is 14 Gyr old this would put the
onset of star formation at z ~ 5 in the Einstein-de Sitter
model, z ~ 6 if  m = 0.25 and
m = 0.25 and

 = 0.75. Since star forming galaxies are
observed in abundance at z ~ 3
(Pettini et al. 1998
and references therein) this is conservative. These numbers give
= 0.75. Since star forming galaxies are
observed in abundance at z ~ 3
(Pettini et al. 1998
and references therein) this is conservative. These numbers give
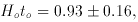 (12)
(12)
where the standard deviations have been added in quadrature.
The result agrees with the low density models in
equation (10). The Einstein-de Sitter case is
off by 1.6 standard deviations, not a serious discrepancy. It
could be worse:
Pont et al. (1998)
put the minimum stellar
evolution age at 13 Gyr. With 1 Gyr for star formation this would
make the Einstein-de Sitter model > 2.6 off. It could go
the other way: an analysis of the distance scale implied by the
geometry of the multiply lensed system PG 1115+090 by
Keeton & Kochanek
(1997)
puts the Hubble parameter at h = 0.51 ± 0.14. At
t0 = 14 Gyr this says
H0t0 = 0.73 ± 0.20, nearly
centered on the Einstein-de Sitter value. An elegant argument
based on the globular cluster distance to the Coma Cluster of
galaxies leads to a similar conclusion
(Baum 1998).
Most estimates of H0 are larger, however, and the correction
to t0 for the time to abundant star formation is
conservative,
so in line 1b of Table 2 I give the
Einstein-de Sitter model a modest demerit for its expansion time.
off. It could go
the other way: an analysis of the distance scale implied by the
geometry of the multiply lensed system PG 1115+090 by
Keeton & Kochanek
(1997)
puts the Hubble parameter at h = 0.51 ± 0.14. At
t0 = 14 Gyr this says
H0t0 = 0.73 ± 0.20, nearly
centered on the Einstein-de Sitter value. An elegant argument
based on the globular cluster distance to the Coma Cluster of
galaxies leads to a similar conclusion
(Baum 1998).
Most estimates of H0 are larger, however, and the correction
to t0 for the time to abundant star formation is
conservative,
so in line 1b of Table 2 I give the
Einstein-de Sitter model a modest demerit for its expansion time.
The low density cases pass the time-scale constraint at the
accuracy of the present measurements. Since a satisfactory and
it is to be hoped feasible measurement would distinguish between the
 m ~ 0.25
open and flat cases I lower their
grades from this test to
m ~ 0.25
open and flat cases I lower their
grades from this test to  ?.
?.



 > 0 and positive
space curvature, and, if the universe is going to contract by a
substantial factor before bouncing, very large space curvature and small
matter density: the redshift at
the bounce is zmax ~ |
> 0 and positive
space curvature, and, if the universe is going to contract by a
substantial factor before bouncing, very large space curvature and small
matter density: the redshift at
the bounce is zmax ~ | R| /
R| /  m.
The bounce case is seldom mentioned, and I suspect rightly so, for
apart from the bizarre initial conditions the redshift
zmax required for light element production requires
quite unacceptable density parameters. If this assessment is
valid we are left with Friedmann-Lemaître solutions that trace back to
infinite density, which is bizarre enough but maybe can be
finessed by inflation and resolved by better gravity physics.
m.
The bounce case is seldom mentioned, and I suspect rightly so, for
apart from the bizarre initial conditions the redshift
zmax required for light element production requires
quite unacceptable density parameters. If this assessment is
valid we are left with Friedmann-Lemaître solutions that trace back to
infinite density, which is bizarre enough but maybe can be
finessed by inflation and resolved by better gravity physics.



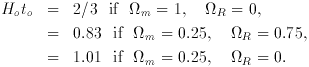
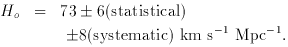
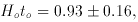
 off. It could go
the other way: an analysis of the distance scale implied by the
geometry of the multiply lensed system PG 1115+090 by
off. It could go
the other way: an analysis of the distance scale implied by the
geometry of the multiply lensed system PG 1115+090 by
 ?.
?.