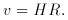
The redshift-distance relation for type Ia supernovae gives an elegant demonstration of this relation ([1], [2]). Arp ([21], [22]) points out that such precision tests do not directly apply to the quasars, and he finds fascinating evidence in sky maps for associations of quasars with galaxies at distinctly lower redshifts. But there is a counterargument, along lines pioneered by Bergeron [23], as follows.
A quasar spectrum may contain absorption lines characteristic of
a cloud of neutral atomic hydrogen at surface density
 HI
HI  3 x 1017 atoms
cm-2. If this
absorption system is at redshift z
3 x 1017 atoms
cm-2. If this
absorption system is at redshift z  1 a galaxy at the
same redshift is close enough that there is a reasonable chance
observing it, and with high probability an optical image does
show a galaxy close to the quasar and at the redshift of the
absorption lines
([24],
[25]).
Also, when a galaxy image
appears in the sky close to a quasar at higher redshift then with
high probability the quasar spectrum has absorption lines at the
redshift of the galaxy. We have good evidence the galaxy is
at the distance
indicated by its redshift. We can be sure the quasar is behind
the galaxy: the quasar light had to have passed through the
galaxy to have produced the absorption lines. If quasars were not
at their cosmological distances we
ought to have examples of a quasar appearing close to the
line of sight to a lower redshift galaxy and without the
characteristic absorption lines produced by the gas in and around
the galaxy.
1 a galaxy at the
same redshift is close enough that there is a reasonable chance
observing it, and with high probability an optical image does
show a galaxy close to the quasar and at the redshift of the
absorption lines
([24],
[25]).
Also, when a galaxy image
appears in the sky close to a quasar at higher redshift then with
high probability the quasar spectrum has absorption lines at the
redshift of the galaxy. We have good evidence the galaxy is
at the distance
indicated by its redshift. We can be sure the quasar is behind
the galaxy: the quasar light had to have passed through the
galaxy to have produced the absorption lines. If quasars were not
at their cosmological distances we
ought to have examples of a quasar appearing close to the
line of sight to a lower redshift galaxy and without the
characteristic absorption lines produced by the gas in and around
the galaxy.
Arp's approach to this issue is important, but I am influenced by what seems to be this direct and clear interpretation of the Bergeron effect, that indicates redshift is a good measure of distance for quasars as well as galaxies.


