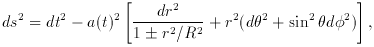
where the expansion rate satisfies the equation
which might be approximated as
The last equation defines the fractional contributions to the
square of the present Hubble parameter H0 by matter, space
curvature, and the
cosmological constant (or a term in the stress-energy tensor that
acts like one). The time-dependence assumes pressureless matter
and constant
By 1930 people understood how one would test the space-time
geometry in these equations, and as I mentioned there is at last
direct evidence for the detection of one of the effects, the
curvature of the relation between redshift and apparent magnitude
([1],
[2]).
As indicated in line 1b, the measured curvature is
inconsistent with the Einstein-de Sitter model in which
In a previous volume in this series Krauss
[28]
discusses the time-scale issue. Stellar
evolution ages and radioactive decay ages do not rule out the
Einstein-de Sitter model, within the still considerable
uncertainties in the measurements, but the longer expansion time
scales of the low
In the analysis by Falco et al.
[29] of the rate
of lensing of quasars by foreground galaxies (line 1d) for a
combined sample of lensing events detected in the optical and
radio, the 2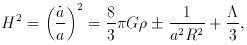
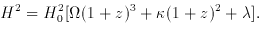
 . Other
notations are in the literature;
a common practice in the particle physics community to add
the matter and
. Other
notations are in the literature;
a common practice in the particle physics community to add
the matter and  terms in a
new density parameter,
terms in a
new density parameter,
 ' =
' =  +
+  . I prefer keeping them separate,
because the observational signatures of
. I prefer keeping them separate,
because the observational signatures of  and
and  can be quite different.
can be quite different.
 = 1
and
= 1
and  = 0 =
= 0 =
 . The
measurements also disagree with a
low density model with
. The
measurements also disagree with a
low density model with  = 0,
though the
size of the discrepancy approaches the size of the error flags,
so I assign a weaker failing grade for this case.
The measurements are magnificent. The
issue yet to be thoroughly debated is whether
the type Ia supernovae observed at redshifts 0.5
= 0,
though the
size of the discrepancy approaches the size of the error flags,
so I assign a weaker failing grade for this case.
The measurements are magnificent. The
issue yet to be thoroughly debated is whether
the type Ia supernovae observed at redshifts 0.5  z
z  1
are drawn from essentially the same population as the nearer ones.
1
are drawn from essentially the same population as the nearer ones.
 models
certainly relieve the problem of
interpretation of the measurements. Thus I enter a
tentative negative grade for the Einstein-de Sitter model in line 1a.
models
certainly relieve the problem of
interpretation of the measurements. Thus I enter a
tentative negative grade for the Einstein-de Sitter model in line 1a.
 bound on the
density parameter in a
cosmologically flat (
bound on the
density parameter in a
cosmologically flat ( = 0) universe
is
= 0) universe
is  > 0.38. The SNeIa
redshift-magnitude
relation seems best fit by
> 0.38. The SNeIa
redshift-magnitude
relation seems best fit by  =
0.25,
=
0.25,  = 0.75, a
possibly significant discrepancy. A serious uncertainty in the
analysis of the lensing rate is the number density of early-type
galaxies in the high surface density branch of the fundamental
plane at luminosities L ~ L*, the luminosity of the
Milky Way. If further tests confirm an inconsistency of the
lensing rate and the redshift-magnitude relation the
lesson may be that
= 0.75, a
possibly significant discrepancy. A serious uncertainty in the
analysis of the lensing rate is the number density of early-type
galaxies in the high surface density branch of the fundamental
plane at luminosities L ~ L*, the luminosity of the
Milky Way. If further tests confirm an inconsistency of the
lensing rate and the redshift-magnitude relation the
lesson may be that  is
dynamical, rolling to zero, as Ratra & Quillen
[30] point out.
is
dynamical, rolling to zero, as Ratra & Quillen
[30] point out.


