


3.2 Biasing and Large-Scale Velocities
The relation between the mass density parameter  and the
gravitational motions of the galaxies is an issue
rich enough for a separate category in
Table 1. It has been
known for the past decade that if galaxies were fair tracer of
mass then the small-scale relative
velocities of the galaxies would imply that
and the
gravitational motions of the galaxies is an issue
rich enough for a separate category in
Table 1. It has been
known for the past decade that if galaxies were fair tracer of
mass then the small-scale relative
velocities of the galaxies would imply that  is well
below unity [3].
If the mass distribution were
smoother than that of the galaxies, the smaller mass
fluctuations would require a
larger mean mass density to gravitationally produce the observed
galaxy velocities. Davis, Efstathiou, Frenk & White
[31]
were the first to show that such a biased distribution of galaxies
relative to mass readily follows in numerical N-body
simulations of the growth of structure, and the demonstration has
been repeated in considerable detail
([32],
[33],
and references therein). This is a serious argument
for the biasing effect. But here are three arguments for
the proposition that galaxies are fair tracers of mass for the
purpose of estimating
is well
below unity [3].
If the mass distribution were
smoother than that of the galaxies, the smaller mass
fluctuations would require a
larger mean mass density to gravitationally produce the observed
galaxy velocities. Davis, Efstathiou, Frenk & White
[31]
were the first to show that such a biased distribution of galaxies
relative to mass readily follows in numerical N-body
simulations of the growth of structure, and the demonstration has
been repeated in considerable detail
([32],
[33],
and references therein). This is a serious argument
for the biasing effect. But here are three arguments for
the proposition that galaxies are fair tracers of mass for the
purpose of estimating  .
.
First, in many numerical simulations dwarf galaxies are less
strongly clustered than giants. This is reasonable, for if much
of the mass were in the voids defined by the giant galaxies, as
required if  = 1, then surely
there would be remnants of
the suppressed galaxy formation in the voids, irregular galaxies
that bear the stigmata of a hostile early environment. The first
systematic redshift survey showed that the distributions of low
and high luminosity galaxies are strikingly similar
[34]. No
survey since, in 21-cm, infrared, ultraviolet, or low surface
brightness optical, has revealed a void population. There is a
straightforward interpretation: the voids are nearly
empty because they contain little mass.
= 1, then surely
there would be remnants of
the suppressed galaxy formation in the voids, irregular galaxies
that bear the stigmata of a hostile early environment. The first
systematic redshift survey showed that the distributions of low
and high luminosity galaxies are strikingly similar
[34]. No
survey since, in 21-cm, infrared, ultraviolet, or low surface
brightness optical, has revealed a void population. There is a
straightforward interpretation: the voids are nearly
empty because they contain little mass.
Second, one can use the galaxy two-point correlation function in
Eq. (1) and the mass autocorrelation function


 from a numerical
simulation of structure formation to define the bias function
from a numerical
simulation of structure formation to define the bias function
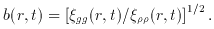 (15)
(15)
In numerical simulations b typically
varies quite significantly with separation and redshift
[32].
That is, the galaxies give a biased
representation of the statistical character of the mass
distribution in a typical numerical simulation. The issue
is whether the galaxies, or the models, or both, are biased
representations of the statistical character of the real mass
distribution. What particularly strikes me is the observation
that the low order galaxy correlation functions have some simple
properties. The galaxy two-point function is close to a power
law over some three orders of magnitude in separation
(Eq. 2). The value of the power law index
 changes little
back to redshift z ~ 1. Within the
clustering length r0 the higher order correlation functions
are consistent with a power law fractal. A reasonable presumption
is that the regularity exhibited by the galaxies reflects a like
regularity in the mass, because galaxies trace mass. I am
impressed by the power of the numerical simulations, and believe
they reflect important aspects of reality, but do not think we
should be surprised if they do not fully represent other aspects,
such as relatively fine details of the mass distribution.
changes little
back to redshift z ~ 1. Within the
clustering length r0 the higher order correlation functions
are consistent with a power law fractal. A reasonable presumption
is that the regularity exhibited by the galaxies reflects a like
regularity in the mass, because galaxies trace mass. I am
impressed by the power of the numerical simulations, and believe
they reflect important aspects of reality, but do not think we
should be surprised if they do not fully represent other aspects,
such as relatively fine details of the mass distribution.
|
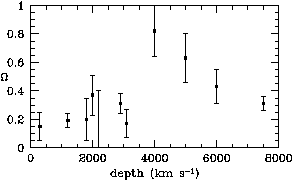
Figure 2. The density parameter derived
from galaxy peculiar
motions on the assumption galaxies trace mass. From the left, the
estimates are based on the Local Group of galaxies, clusters of
galaxies, the peculiar infall toward the Virgo Cluster
[35],
and the analyses in references
[36] to
[38].
|
The third argument deals with the idea that blast waves or
radiation from the formation of a galaxy may have affected the
formation of nearby galaxies, producing scale-dependent bias. In
this case the apparent value of the density parameter derived
from gravitational motions within systems of galaxies on the
assumption galaxies trace mass would be
expected to vary with increasing scale, approaching the true
value when derived from relative motions on scales larger than
the range of influence of a forming galaxy.
Fig. 2 shows a test.
The abscissa at the entry for clusters of galaxies is the
comoving radius of a sphere that contains the mass within the
Abell radius. The estimates at larger scales are plotted at
approximate values of the radius of the sample. If it were not
for the last two points at the right-hand side of
Fig. 2,
one might conclude that the apparent density parameter is
increasing to the true value  ~ 1 at
R ~ 50h-1 Mpc. But considering the last two points,
and the sizes of the error flags, it is difficult to
see any evidence for scale-dependent bias.
~ 1 at
R ~ 50h-1 Mpc. But considering the last two points,
and the sizes of the error flags, it is difficult to
see any evidence for scale-dependent bias.
I assign a strongly negative grade for the Einstein-de Sitter
model in line 2a in Table 1, based
on galaxy motions on relatively small scales, because biasing
certainly is required if  = 1
and I have argued there
is no evidence for it. The more tentative grade in line 2b is
based on Fig. 2: the apparent value of the
density parameter does
not seem to scale with depth.
= 1
and I have argued there
is no evidence for it. The more tentative grade in line 2b is
based on Fig. 2: the apparent value of the
density parameter does
not seem to scale with depth.



 and the
gravitational motions of the galaxies is an issue
rich enough for a separate category in
Table 1. It has been
known for the past decade that if galaxies were fair tracer of
mass then the small-scale relative
velocities of the galaxies would imply that
and the
gravitational motions of the galaxies is an issue
rich enough for a separate category in
Table 1. It has been
known for the past decade that if galaxies were fair tracer of
mass then the small-scale relative
velocities of the galaxies would imply that  is well
below unity [3].
If the mass distribution were
smoother than that of the galaxies, the smaller mass
fluctuations would require a
larger mean mass density to gravitationally produce the observed
galaxy velocities. Davis, Efstathiou, Frenk & White
[31]
were the first to show that such a biased distribution of galaxies
relative to mass readily follows in numerical N-body
simulations of the growth of structure, and the demonstration has
been repeated in considerable detail
([32],
[33],
and references therein). This is a serious argument
for the biasing effect. But here are three arguments for
the proposition that galaxies are fair tracers of mass for the
purpose of estimating
is well
below unity [3].
If the mass distribution were
smoother than that of the galaxies, the smaller mass
fluctuations would require a
larger mean mass density to gravitationally produce the observed
galaxy velocities. Davis, Efstathiou, Frenk & White
[31]
were the first to show that such a biased distribution of galaxies
relative to mass readily follows in numerical N-body
simulations of the growth of structure, and the demonstration has
been repeated in considerable detail
([32],
[33],
and references therein). This is a serious argument
for the biasing effect. But here are three arguments for
the proposition that galaxies are fair tracers of mass for the
purpose of estimating  .
.





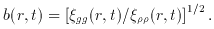
 changes little
back to redshift z ~ 1. Within the
clustering length r0 the higher order correlation functions
are consistent with a power law fractal. A reasonable presumption
is that the regularity exhibited by the galaxies reflects a like
regularity in the mass, because galaxies trace mass. I am
impressed by the power of the numerical simulations, and believe
they reflect important aspects of reality, but do not think we
should be surprised if they do not fully represent other aspects,
such as relatively fine details of the mass distribution.
changes little
back to redshift z ~ 1. Within the
clustering length r0 the higher order correlation functions
are consistent with a power law fractal. A reasonable presumption
is that the regularity exhibited by the galaxies reflects a like
regularity in the mass, because galaxies trace mass. I am
impressed by the power of the numerical simulations, and believe
they reflect important aspects of reality, but do not think we
should be surprised if they do not fully represent other aspects,
such as relatively fine details of the mass distribution.
