2.1.3. Mass-to-light Ratio of the Spheroid Component
The mass-to-light ratio of stars and
their remnants in spheroid populations can be inferred from
star population synthesis calculations, assuming the stars are
close to coeval (so that the integrated B luminosity is not much
affected by recent episodes of star formation)
and the spheroid stars in our neighborhood are representative.
Within these assumptions the most serious uncertainty
in the calculation is the lower cut off
of the initial mass function (the IMF). In the past the cutoff was
somewhat arbitrary, between 0.1 M
and 0.2 M, and
the choice seriously affected
the estimate of M/L. Thus for the Salpeter IMF
M differs by 24% between these two
choices, while L is virtually unaffected. This uncertainty
for the local IMF has been removed by the recent advance
in observation of M subdwarf star counts with the Hubble Space Telescope:
it has been shown that the IMF of the local Galactic stars
has a turnover at about 0.4 M
(Gould, Bahcall & Flynn
1996;
hereafter GBF), and the integral over the
GBF mass
function converges without an arbitrary cut off. For M >
M
the GBF mass function
agrees well with the Salpeter function.
Using the GBF mass
function for M < M, instead of the
Salpeter mass function with x = 1.35 (where x is the index of the
IMF dn/dM 
M-[1+x]),
the mass integral is 0.70 times that obtained with the Salpeter mass
function cut off at 0.15 M.
The light in the blue-visual bands contributed by stars less
massive than one solar mass is
small: from Table 4 of
Tinsley & Gunn (1976),
we estimate that
the V light integral decreases only 2% with the use of the
GBF
mass function. Therefore, the mass-to-light ratio with the
GBF mass
function is (M/LV)GBF = 0.72
(M/LV)Salpeter,
where the latter ratio is computed for the cutoff at
0.15 M.
Charlot, Worthey, &
Bressan (1996)
have given a
compilation of mass-to-light ratios from various stellar
population synthesis calculations. They show that
M/LV is reasonably consistent among authors when
the lower mass cutoff is fixed. From the
Charlot et al. (1996)
compilation of population synthesis calculations,
the GBF IMF, and the
conversion formula discussed above, we obtain
(M/LV)GBF = (4.0 ± 0.3) + 0.38
(tG - 10 Gyr), where
tG is the age of the spheroid and the error represents the
model-dependent uncertainty. Using the
Charlot et al. (1996)
synthetic calculation of the B - V color, we obtain
M/LB = (5.4 ± 0.3) + 0.7 (tG -
10 Gyr).
For tG = 12 ± 2 Gyr we have
M/LV = 4.0-5.9, or
The M/L ratio in equation (5) may be compared to
the values inferred from the kinematics of the nuclear regions of
elliptical galaxies.
van der Marel (1991)
finds M/LR = (6.64 ± 0.28)h (Johnson R),
which translates to M/LV = (7.72 ± 0.33)h or
using < V - RJ > = 0.68,
corresponding to the average color < B - V > = 0.92 for
the 37 elliptical galaxies he used (< B - V >
Dynamical measures show M/L depends on the luminosity in
elliptical galaxies
(Kormendy 1986):
van der Marel (1991)
finds M/L = (L/L*)0.35 ±
0.05. This manifestation
of the color-magnitude relation of early-type galaxies
probably reflects the effect of metallicity and perhaps also
of dark matter halos. In the former case we estimate
this dependence may reduce the effective mean value of M/L
weighted by the contribution to the luminosity density by 17%,
and accordingly reduce the lower end of the allowed range by
this amount.
We conclude that a good estimate of the mass-to-light ratio of
stars and their remnants in spheroids is
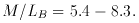
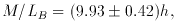
= 0.65 and
< V - RJ > = 0.52 are also used).
There is excellent consistency between equations (5)
and (6) if the Hubble constant is in the range
h = 0.6-0.8 and spheroid populations dominate the the mass
of these nuclear regions.
