To draw lessons for cosmology, we need not only the physical properties of individual clusters but also an understanding of how typical the numbers are. The issue here is whether the Abell catalog or any other now available is adequate for the purpose. There are known problems in the catalogs: they contain objects with suspiciously low velocity dispersions, and they miss systems whose X-ray properties might be consistent with massive clusters.
Recently there has been considerable interest in the possible systematic errors this might introduce in estimates of cluster masses and spatial correlations (Sutherland 1988; Kaiser 1989; Dekel et al. 1989; Frenk et al. 1989). The points are well taken but I think the situation is not disastrous: if we take a balanced view, not attempting to push the data too hard, and taking care to look for supporting evidence from tests of reproducibility, we get some believable and useful measures.
The cluster-galaxy cross correlation function, 1 +
cg(r),
is the mean number density
of galaxies as a function of distance r from a cluster, measured
in units of the large-scale
mean density. The fact that one finds consistent estimates of
cg from
different cluster
distance classes (with reasonable choice of parameters in the luminosity
function) is
evidence that the typical richness of the cluster sample does not vary
substantially with
distance. The number of bright galaxies within the Abell radius
ra = 1.5h-1 Mpc (H =
100h km sec-1 Mpc-1) around a cluster is
larger than expected for a homogeneous distribution by the factor
|
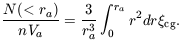
The original estimate (Seldner and Peebles 1977) is N(< ra) / nVa = 360; the reanalysis by Lilje and Efstathiou (1988), which uses better cluster distances and galaxy luminosity function, is half that. I adopt the mean with twice the weight for the newer value:
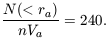
| (1) |
The scatter around the mean value of N(< ra) surely is
large, even for a given
nominal richness class, because richness estimates are compromised by
groups and clusters
seen in projection. The rms scatter in N(< r) from cluster to
cluster is measured
by the cluster-galaxy-galaxy correlation function,
cgg
(Fry and Peebles
1980).
Estimates of
cgg should
be reworked using the better current distance scales and luminosity
function; the old result is
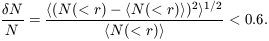
| (2) |
This is substantial, but still it indicates that we can trust equation (1) to a factor of two for the overdensity of a typical richness class 1 cluster.
We can compare equation (2) to the scatter in estimates of the velocity
dispersion
v2 for Abell clusters. The average over the estimates
of v2 for the 54 R
1 clusters in
the Struble and
Rood (1987)
compilation is
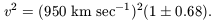
| (3) |
The last factor is the fractional rms scatter in the estimates of v2 among the 54 clusters. The scatter surely has been inflated by the cosmological redshift differences of objects accidentally close in projection (and perhaps suppressed by over-enthusiastic pruning of the tails of the velocity distribution). However, the coincidence of the fractional scatter in v2 and the bound for N (eq. [2]) is consistent with the assumption that the scatter in velocity dispersions is dominated by the scatter in masses of the clusters rather than measuring errors.
Arguing for the same conclusion is the fact that most clusters are X-ray sources, and that where the X-ray gas temperature is known it is about what would be expected if the plasma and galaxies had the same temperature. For example, in Mushotzky's (1984) sample, clusters with X-ray temperature ~ 100.6 keV have galaxy line of sight velocity dispersions in the range 900 ± 300 km sec-1, compared to the expected value 800 km sec-1 for equal temperatures. Part of the scatter surely comes from temperature differences between plasma and galaxies and from variations of temperature with position, but the key point for our purpose is that there is not a lot of room for spurious estimates of the typical cluster velocity dispersion.
As a final check, let us estimate the cosmological mean mass density from these numbers. Since the velocity dispersion in a cluster tends to drop with increasing distance from the center, and equation (3) surely has been somewhat inflated by random errors in the measurements of v, a reasonable estimate of the rms line of sight velocity dispersion at the Abell radius is 750 km sec-1. In the isothermal gas sphere model, this makes the mass within the Abell radius
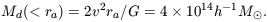
| (4) |
If galaxies traced the large-scale mass distribution, then the contrast in galaxy counts in equation (1) would be the same as the mass contrast:
|
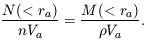
With equation (4) this fixes the mean mass density,
, which translates to the
cosmological density parameter
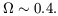
| (5) |
The more direct way to get at this number is to find masses and
luminosities of individual clusters. For example,
Hughes (1989)
finds for the Coma Cluster a mass to light
ratio ~ 300h solar units. This multiplied by the mean luminosity
density gives 
~ 0.3,
a commonly encountered number from this method. Very similar numbers
follow from masses derived from luminous arcs
(Grossman and
Narayan 1989,
Hammer and Rigault
1989).
The value of this effective
thus is secure, and the
consistency with equation (5) is a positive check of equations (1) and (4).
There are three notable results from these observations. First, there is a hard upper cutoff in cluster masses, as evidenced by the fact that the Struble-Rood (1987) catalog lists just one cluster with estimated v2 ~ three times the mean in equation (3). That is, Nature is adept at placing the mass in equation (4) into a radius of 1.5h-1 Mpc, but quite reluctant to place three times that amount in the same volume. (The analogous effect for galaxies is the upper cutoff in circular velocity at r ~ 10 kpc at about twice that of our galaxy.) This cluster mass cutoff might be expected in theories for cluster formation out of Gaussian primeval density fluctuations, because the upper envelope of Gaussian fluctuations is tightly bounded. In cosmic string theories the effect is more problematic, because clusters are supposed to be seeded by loops that have a broad range of masses. However, Zurek (1988) argues that with suitable parameter choices the predicted spread in cluster masses may agree with the observations.
Second, the mass Md in equation (4) is at the upper end of the range of masses Mx of the X-ray producing gas (Jones and Foreman 1984). The fact that Mx typically is less than Md illustrates the familiar point that clusters generally are dominated by dark mass. It will be interesting to see whether there are clusters in which the dynamical mass within the Abell radius may be accounted for by the mass needed to produce the X-rays. If so, then theories that assume the universe is dominated by weakly interacting matter initially well mixed with the baryons would a require considerable settling of the plasma, an effect that might be testable by the methods described at these Proceedings by Evrard.
Third, as we have noted in equation (5), if the mean mass per galaxy in clusters applied to all galaxies, the mean mass density would be less than the simple (and currently fashionable) Einstein-de Sitter cosmology with negligibly small space curvature and cosmological constant. The possible relation to galaxy formation theories is discussed in Section II below.
Galaxy formation theories also are tested by the spatial clustering of
clusters, as
measured by the usual N-point correlation functions. As for any other
statistic, the way
to decide whether the cluster-cluster two-point function,
cc, is
reliably detected is to
test for reproducibility of results from independent samples and from
different ways of
analyzing the same sample. The hope is that these different approaches
are differently
affected by systematic errors, so errors would be revealed as
significant discrepancies
in the statistic. Thus Mike Hauser and I decided that we had a
believable detection of
clustering because we found that the two-point angular function,
wcc(
), in the
Abell (1958)
catalog scales with distance about as expected for a
spatially homogeneous random process.
Bahcall and Soneira (1983) introduced the use of the standard fitting form for the two-point function:
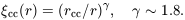
| (6) |
The angular two-point function gives hrcc ~ 28 ± 7 Mpc (Hauser and Peebles 1973). Bahcall's (1988) estimate, based mainly on redshift samples, is 23 ± 3 Mpc. The angular and redshift correlation functions use the same catalog but in different ways, that one might have expected would be differently affected by spurious clustering introduced in the discovery of the clusters. The rough consistency of these estimates of rcc thus argues for the reality of the clustering. The same comments apply to the deeper redshift sample of Postman (1989), which gives 19+7-4, and the X-ray selected sample of Lahav et al. (1989), which gives 19 ± 4 Mpc. The mean of these four estimates is
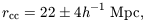
| (7) |
where I have taken the precaution of doubling the formal standard deviation of the mean.
Dekel et al. (1989) argue that the clustering of Abell clusters may be an artifact of projection contamination. The case for contamination at some level is persuasive, but of course their model for the effect need not usefully approximate the way people actually discover clusters. My conclusion from the reproducibility of rcc is that projection effects are a second order correction, that there is a strong case for the reality of clustering at the level of equation (7). With the Hubble constant H = 50 km sec-1 Mpc-1 favored by the biased cold dark matter theory (Frenk et al. 1989), the mass autocorrelation function vanishes at r ~ 70 Mpc, about 50 percent larger than rcc. Thus the cold dark matter theory does not directly contradict equation (7), but in some estimates the margin is uncomfortably close (Blumenthal, Dekel and Primack 1988).