As discussed above, the mean mass per galaxy in a great cluster is about 30% of the global mean for the Einstein-de Sitter model. This difference might be telling us something about cosmology, or about the formation and evolution of clusters.
Two commonly cited processes after cluster assembly may change the mean mass per galaxy. Gas loss by stripping would lower the luminosities of cluster members and so increase the value of the mass per galaxy brighter than some fixed cutoff. This goes the wrong way if we want an Einstein-de Sitter universe. West and Richstone (1988) note that dynamical relaxation would tend to raise the galaxy concentration in the cluster center, and so lower the mean mass per galaxy, which is in the wanted direction. The traditional problem with this is that the same effect might have been expected to have segregated giant galaxies from dwarfs, and to have driven the intracluster plasma out of the center of the cluster. Neither effect could be considered to be manifestly present in clusters: the plasma mass in some clusters is larger than the mass in the bright parts of galaxies, and, as discussed in these Proceedings by Sandage and by Haynes, clusters contain a high relative abundance of apparently low mass galaxies. Thus my impression of the evidence is that the low mass per galaxy in clusters probably was present at creation, as bias in galaxy formation, or because the mean density of the universe is low.
In massive cosmic string theories, a cluster forms by gravitational
accretion around a large cosmic string loop
(Turok 1985).
Since the large loops would come from a
generation well removed from the progenitors of galaxies, it would be
reasonable to
expect that the positions of the large loops are not strongly correlated
with the positions
of galaxies. It would follow that the large loop on average collects a
fair sample of mass
and galaxies. Thus the low value of equation (5), if primeval, is a
serious problem for massive cosmic string pictures with density parameter
= 1. One way out is to suppose
that some component of the dark mass has pressure high enough to resist
accretion by
the cluster; decaying dark matter is a possibility (e.g.,
Suto, Kodama and
Sato 1987).
In cosmic string theories with hot dark matter (neutrinos with mass of a
few tens
of electron volts, as discussed e.g., by
Brandenberger,
Perivolaropoulos and Stebbins 1989),
galaxies would be assembled at low redshifts, and the biasing
mechanism to
be discussed next might be relevant. There has not yet been much
discussion of the
possibility of applying the cosmic string picture in a low density world model.
In the biased galaxy formation picture, one argues that galaxies may have formed at higher than average efficiency in the generally overdense region of a protocluster (Frenk et al. 1989 and references therein), thus lowering the mean mass per cluster member. It may be possible to test this, because in a dense universe a massive cluster once formed continues to grow by gravitational accretion, as we see in virgocentric flow. In an Einstein-de Sitter universe, this accretion doubles the mass of a cluster from redshift z = 1 to the present. If the mass per galaxy were biased low within the cluster at formation, then it would be reasonable to expect that the cluster subsequently grew by accretion of material with a higher mass per galaxy. (This is required in the global average; it might be expected to apply to the galaxies in the immediate neighborhood of a cluster because they would have formed at lower density and hence at lower efficiency than in the central parts of the cluster.) Since the material accreted at low redshifts would tend to be found in the outer parts of the cluster, the biasing picture would predict that the mass per galaxy increases with increasing distance from the cluster center.
Measurements of cluster masses have greatly improved with the addition of
X-ray observations (as discussed by Forman at this conference) and the
observations of gravitationally lensed images
(Grossman and
Narayan 1989,
Hammer and Rigaut
1989),
but tests of the predicted radial variation of the ratio
(r) / n(r) of
mass density
to galaxy number density unfortunately still are limited by the
relatively small range
of radii of the observations. One could design a measurement of the
ensemble average
values of (r)
and n(r) as functions of radius r, using the equilibrium
condition familiar from stellar dynamics,
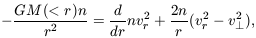
| (8) |
where v2r(r) and
v2
(r) are the mean square values
of the radial and one dimensional
transverse galaxy velocities as functions of distance r from the
cluster center, and
n(r) is proportional to the cluster-galaxy cross correlation
function
cg(r)
discussed
above. It will be noted that individual clusters are not assumed to have
any particular
symmetry; equation (8) applies to the ensemble average under the
assumption that
the mean density is constant over a dynamical time. There is the usual
problem that the velocity anisotropy is unknown. If
v were small,
the mass would be smaller than
is indicated by the isotropic case in equation (4), which means equation
(4) would
overestimate the mass per galaxy. The bias in the other direction is
relatively small,
saturating at circular orbits. That is, a low apparent mass per galaxy
in the outer parts
of clusters would be a significant and exceedingly interesting challenge
for biasing. To
apply equation (8), one would need a fair sample of galaxy redshifts
around a fair
sample of clusters. The practical problem is that a substantial fraction
of the redshift
measurements at large projected distances from a cluster center would be
'wasted' on background and foreground galaxies.