2.1. The Cosmological Principle
It is meaningful to talk of cosmic or universal radiation fields, rather than the radiation received from this or that system in a hierarchy of structures, because the evidence is that the universe we can see back to high redshift is close to homogeneous and isotropic. I discuss here some of the evidence and the measures of large-scale departures from homogeneity.
A useful foil to the standard homogeneous world picture models the large-scale distribution of matter as a scale-invariant fractal with dimension D. If D < 2 the mean column density of material along a line of sight converges, meaning there is no Olbers paradox of unbounded sky brightness even if the universe were static and stars lived forever. This case is easy to rule out, however, because the angular distribution of the column density of material integrated to distance R has the same fractal dimension D, independent of R (as one must expect, for in a scale-invariant fractal there is no characteristic length to set the scale for R). That is, the angular fluctuations in counts of objects across the sky are statistically independent of the depth to which the objects are counted, which is quite contrary to the observations. (This prediction and its observational tests are discussed in sections 3 and 7 of Principles of Physical Cosmology, Peebles 1993, hereafter PC).
If 2 < D < 3 the line-of-sight integral for the background radiation surface brightness has to be cut off at some limiting distance Rlim, by the finite lifetime of the sources or by the cosmological redshift. We know an appreciable fraction of the X-ray background (the XRB) is produced by sources with redshifts on the order of unity, that is, that in this case Rlim is on the order of the Hubble distance cH0-1 = 3000h-1 Mpc (where H0 = 100h km s-1 Mpc-1). It is an easy exercise to check that in a scale-invariant fractal model with 2 < D < 3, and with sources turned off at distances greater than Rlim, the quadrupole anisotropy of the integrated background is
| (1) |
again independent of Rlim. The large-scale anisotropy of the XRB is not more than a few tenths of one percent, meaning that the fractal dimension of the large-scale space distribution of X-ray sources differs from D = 3 by only a few parts in 1000.
The bound on D is removed if we are close to the center of a universe spherically symmetric about one position, but since our galaxy and its near neighbors appear to be quite ordinary this does not seem to be a very sensible model.
The large-scale isotropy of the 3 K thermal cosmic background radiation
(the CBR)
gives an even better limit on large-scale mass fluctuations, if we are
willing to assume
general relativity theory is a useful approximation to physics on the
scale of the Hubble
length. Here a useful foil assumes mass cluster with galaxies on scales
~ 10h-1 Mpc,
and that the mass autocorrelation function
(r) =
< 
(
+
)
() > /
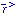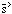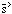< >2 - 1
vanishes at
larger separations. Then the large-scale rms density fluctuations are
characterized by the integral
| (2) |
The second line is based on the galaxy two-point correlation
function. In this model
the rms fluctuation in the mass in a randomly placed sphere of radius
r large compared
to the support of is
| (3) |
and the rms value of the velocity averaged over the material within the sphere is (PC Sections 13 and 21)
| (4) |
The cosmological density parameter
is the ratio of the mean mass
density to the
critical Einstein-de Sitter value. The indicated scaling with
is a good approximation if
the cosmological constant 
vanishes or if is present
and space curvature is negligible.
The numbers in equations (3) and (4) are comparable to the direct
estimates from galaxy counts and galaxy peculiar motions.
In this model for the mass distribution, and with an Einstein-de Sitter cosmological model, the CBR quadrupole anisotropy produced by the gravitational potential fluctuations at the Hubble distance (the Sachs-Wolfe effect) is
| (5) |
an order of magnitude above the COBE quadrupole anisotropy Mather and Vittorio discuss in these Proceedings.
The lesson is that our model gives a not unreasonable picture for the
mass fluctuations
on scales 
100 Mpc, but
it significantly overestimates fluctuations on larger
scales. An equivalent way to put it is that the power spectrum of mass
fluctuations has
to decrease with increasing scale at wavelengths
100 Mpc. This was predicted by
the inflation theory incorporated in the adiabatic Cold Dark Matter
cosmogony
(Frenk 1991
and references therein), an impressive success. One should bear in mind,
however,
that the wanted decrease in the mass fluctuation spectrum at large
separations appears in other scenarios, such as cosmic strings and textures
(Turok 1991).
Equation (5) does assume general relativity theory, and it would be very interesting to have a check on this constraint from a direct measurement of the fluctuations in the distribution of sources on the scale of the Hubble length. The constraint says the fluctuations are less than one part in 104, however, which will not be easy to get at.
A related issue is the interpretation of the CBR dipole anisotropy. The COBE measurements described by Mather show that the CBR anisotropy is very close to a pure dipole in thermodynamic temperature. This is consistent with the usual assumption that the dipole is caused by our peculiar motion relative to the general Hubble expansion of the universe, that is, that the rest frame defined by the CBR agrees with the rest frame defined by the mean motion of the matter within the Hubble length. Detection of the departure from a pure dipole due to the second-order Doppler shift would be an important check, but I gather not yet within reach.
A detection of the mass fluctuations whose gravitational pull drive our motion relative to the CBR would be a key test of the velocity interpretation. One can estimate the peculiar gravitational acceleration caused by the galaxies taken to be tracers of the mass within distance R. If the direction and magnitude of the acceleration are unchanged as R is increased, and agree with our motion relative to the CBR for a sensible value of the mass per tracer galaxy, one has reason to believe the mass fluctuations whose gravity produced our peculiar motion are detected with R. In a recent application, Strauss et al. (1992) find that the direction of the gravitational acceleration of IRAS galaxies taken to be mass tracers converges to within 20° of the CBR dipole direction at H0R ~ 3000 km s-1, and stays within that angular distance as one adds IRAS galaxies out to H0R ~ 20,000 km s-1. This suggests the source of the motion of our Local Group of galaxies is within 3000 km s-1 distance. If that were so, however, one would expect to find an appreciably smaller mean peculiar velocity in the average over the material within a sphere of radius larger than 3000 km s-1, contrary to the present evidence. The mean peculiar velocity relative to the CBR for the galaxies within 6000 km s-1 is about 400 km s-1, directed ~ 40° away from the motion of the Local Group relative to the CBR (Faber and Burstein 1988; Mould et al. 1993). The Postman-Lauer (1993) mean peculiar flow for Abell clusters at R < 15,000 km s-1 has a similar magnitude but swings to ~ 90° from the motion of the Local Group relative to the CBR. In short, our picture for the large-scale peculiar velocity field and the mass density fluctuations that may have caused it remains confused.
It would be very helpful to have a measurement of the XRB dipole. If the CBR dipole were the result of our peculiar motion caused by the gravitational pull of mass fluctuations well within the Hubble length then we would expect to see a parallel dipole anisotropy in the XRB. If on the other hand the CBR dipole were due to a very smooth gradient in the primeval entropy per unit mass the X-ray dipole from sources within the Hubble length would not be expected to stand out above the other low order multipole moments of the XRB, or to be aligned with the CBR dipole. I gather the experts are not yet willing to make a definite pronouncement on this important test.
2.2 The Mean Optical Luminosity Density
My conclusion is that we have a good case for Einstein's cosmological principle, that the universe is close to homogeneous and isotropic in the large-scale average. (1) This means we can consider the mean mass density of the universe, and the mean density of radiation as a function of wavelength. Of particular interest is the quantity de Vaucouleurs (1949) considered, the density of starlight, as a check on our inventory of luminous objects in the universe (Peebles and Partridge 1967). This is motivated by the notorious mass problem in cosmology, that the starlight in the known galaxies, assigned a mass-to-light ratio characteristic of familiar star populations, yields a mass insufficient to account for the motions of galaxies within groups and clusters, and two orders of magnitude below the Einstein-de Sitter density usually considered to be the most reasonable possibility. The commonly discussed interpretation is that the mass of the universe is dominated by nonbaryonic matter, perhaps massive neutrinos or some other weakly interacting particle, maybe something even more exotic. But it behooves us to consider the possibility that our sums have missed luminous objects too compact to be distinguished from stars, or too low in surface density to be seen against the light of the night sky. We have a test, from the comparison of the mean surface brightness contributed by the known galaxies and the measured extragalactic sky brightness (after correction for airglow, the zodiacal light, and the diffuse light of the Milky Way).
Tyson's (1990) value for the mean surface brightness of the sky at 4500 Å from the sum of observed galaxies is
| (6) |
This is de Vaucouleurs' (1949) computation; it is impressive that the result has not changed by more than a factor of about two. The equivalent mean luminosity density is
| (7) |
Mattila's (1990) survey indicates the measured extragalactic sky brightness satisfies
| (8) |
The difference between this and the surface brightness contributed by ordinary galaxies (eq. [6]) leaves room for new classes of objects with luminosity density an order of magnitude greater than that of the known galaxies. With conventional mass-to-light ratios for star populations this leaves the bound on the mass density of luminous material an order of magnitude below the Einstein de-Sitter value.
The relation between equations (6) and (7) is not sensitive to the cosmological model, because the cosmological redshift suppresses the contribution from ordinary galaxies at the Hubble distance. But we see that there is considerable room for galaxy evolution that could have produced ultraviolet emission which has been redshifted into the visible band. Advances in the art of measuring the extragalactic optical and near infrared background, as discussed here by Hauser, thus will be followed with great interest.
1 A lesson from the inflation cosmology is that the universe at great distances could be very different from what we see. The more careful statement thus is that mass density variations across the Hubble length have to be less than about one part in 104. The issue seldom debated is whether Einstein was right for the right reason, and the universe really is close to uniform everywhere. Back.