2. THE CLASSICAL TESTS

2.1. The Physics of the Friedmann-Lemaître Model

The second to the last column in the table summarizes elements of the physics of the relativistic Friedmann-Lemaître cosmological model we want to test.

The starting assumption follows Einstein in taking the observable universe to be close to homogeneous and isotropic. This agrees with the isotropy of the radiation backgrounds and of counts of sources observed at wavelengths ranging from radio to gamma rays. Isotropy allows a universe that is inhomogeneous but spherically symmetric about a point very close to us. I think it is not overly optimistic to consider this picture unlikely, but in any case it is subject to the cosmological tests, through its effect on the redshift-magnitude relation, for example.

It will be recalled that, if a homogeneous spacetime is described by a single metric tensor, the line element can be written in the Robertson-Walker form,

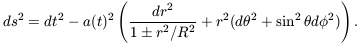
(1)

This general expression contains one constant, that measures the curvature of sections of constant world time t, and one function of t, the expansion parameter a(t). Under conventional local physics the de Broglie wavelength of a freely moving particle varies as a(t). In effect, the expansion of the universe stretches the wavelength. The stretching of the wavelengths of observed freely propagating electromagnetic radiation is measured by the redshift, z, in terms of the ratio of the observed wavelength of a spectral feature to the wavelength measured at rest at the source,

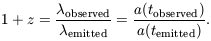
(2)

At small redshift the difference t of world times at emission and detection of the light from a galaxy is relatively small, the physical distance between emitter and observer is close to r = c t, and the rate of increase of the proper distance is

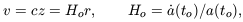
(3)

evaluated at the present epoch, t_o. This is Hubble's law for the general recession of the nebulae.

Under conventional local physics Liouville's theorem applies. It says an object at redshift z with radiation surface brightness i_e, as measured by an observer at rest at the object, has observed surface brightness (integrated over all wavelengths)

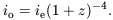
(4)

Two powers of the expansion factor can be ascribed to aberration, one to the effect of the redshift on the energy of each photon, and one to the effect of time dilation on the rate of reception of photons. In a static ``tired light'' cosmology one might expect only the decreasing photon energy, which would imply

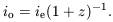
(5)

Measurements of surface brightnesses of galaxies as functions of redshift thus can in principle distinguish these expanding and static models (Hubble & Tolman 1935).

The same surface brightness relations apply to the 3 K thermal background radiation (the CBR). Under equation (4) (and generalized to the surface brightness per frequency interval), a thermal blackbody spectrum remains thermal, the temperature varying as T a(t)^-1, when the universe is optically thin. The universe now is optically thin at the Hubble length at CBR wavelengths. Thus we can imagine the CBR was thermalized at high redshift, when the universe was hot, dense, and optically thick. Since no one has seen how to account for the thermal CBR spectrum under equation (5), the CBR is strong evidence for the expansion of the universe. But since our imaginations are limited, the check by the application of the Hubble-Tolman test to galaxy surface brightnesses is well motivated (Sandage 1992).

The constant R^-2 and function a(t) in equation (1) are measurable in principle, by the redshift-dependence of counts of objects, their angular sizes, and their ages relative to the present. The metric theory on which these measurements are based is testable from consistency: there are more observable functions than theoretical ones.

The more practical goal of the cosmological tests is to over-constrain the parameters in the relativistic equation for a(t),

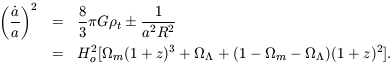
(6)

The total energy density, _t, is the time-time part of the stress-energy tensor. The second line assumes _t is a sum of low pressure matter, with energy density that varies as _m a(t)^-3 (1 + z)³, and a nearly constant component that acts like Einstein's cosmological constant . These terms, and the curvature term, are parametrized by their present contributions to the square of the expansion rate, where Hubble's constant is defined by equation (3).

2.2. Applications of the Tests

When I assembled Table 1 the magnificent program of application of the redshift-magnitude relation to type Ia supernovae was just getting underway, with the somewhat mixed preliminary results entered in line 2c (Perlmutter et al. 1997). Now the supernovae measurements clearly point to low _m (Reiss 2000 and references therein), consistent with most other results entered in the table.

The density parameter _m inferred from the application of equation (6), as in the redshift-magnitude relation, can be compared to what is derived from the dynamics of peculiar motions of gas and stars, and from the observed growth of mass concentrations with decreasing redshift. The latter is assumed to reflect the theoretical prediction that the expanding universe is gravitationally unstable. Lines 1a and 1b show estimates of the density parameter _m based on dynamical interpretations of measurements of peculiar velocities (relative to the uniform expansion of Hubble's law) on relatively small and large scales. Some of the latter indicated _m ~ 1. A constraint from the evolution of clustering is entered in line 3c. The overall picture was pretty clear then, and now seems well established: within the Friedmann-Lemaître model the mass that clusters with the galaxies almost certainly is well below the Einstein-de Sitter case _m = 1. I discuss the issue of how much mass might be in the voids between the concentrations of observed galaxies and gas clouds in Section 4.1.

All these ideas were under discussion, in terms we could recognize, in the 1930s. The entry in line 2e is based on the prediction of gravitational lensing. That was well known in the 1930s, but the recognition that it provides a cosmological test is more recent. The entry refers to the multiple imaging of quasars by foreground galaxies (Fukugita & Turner 1991). The straightforward reading of the evidence from this strong lensing still favors small , but with broad error bars, and it does not yet seriously constrain _m (Helbig 2000). Weak lensing - the distortion of galaxy images by clustered foreground mass - has been detected; the inferred surface mass densities indicate low _m (Mellier et al. 2001), again consistent with most of the other constraints.

The other considerations in lines 1 through 4 are tighter, but the situation is not greatly different from what is indicated in the table and reviewed in Lasenby, Jones & Wilkinson (2000).