


2.1. Electron Impact Excitation
The quantity usually computed for electron impact excitation is
denoted as  (i, j), which
was introduced by
Hebb and Menzel
(1940)
and later termed the ``collision strength'' by Seaton, in analogy with the
line strength for radiative transitions.
The
(i, j), which
was introduced by
Hebb and Menzel
(1940)
and later termed the ``collision strength'' by Seaton, in analogy with the
line strength for radiative transitions.
The  is dimensionless and
symmetric with respect to initial and final states. It is related to the
cross section as
is dimensionless and
symmetric with respect to initial and final states. It is related to the
cross section as
in units of the area of the H atom.
The usually tabulated quantity is the maxwellian averaged collision
strength, also called the effective collision strength,
The excitation rate coefficient, in cm3 sec-1, is
defined as
related to the de-excitation rate coefficient (Ei <
Ej) as
The influence of autoionizing resonances may be seen in
Fig. 2.
Figure 2. Collision strength for the
forbidden transition
6D9/2 - 6D7/2
in Fe II (Pradhan and Zhang 1993). The
A detailed discussion on the analysis of collision strengths and rate
coefficients is given by
Burgess and Tully
(1992),
who describe analytic fitting procedures to
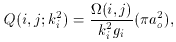
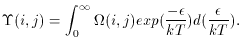
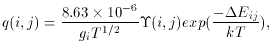
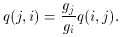
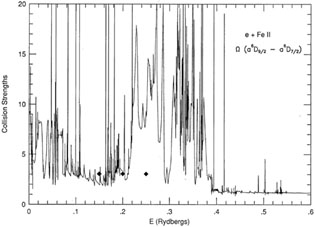
 (T), at T = 10,000
K, using the close coupling
collision strengths shown in Fig. 2 is approximately a factor of
three higher than the one calculated using the distorted wave values
(diamonds) calculated by
Nussbaumer and
Storey (1980).
(T), at T = 10,000
K, using the close coupling
collision strengths shown in Fig. 2 is approximately a factor of
three higher than the one calculated using the distorted wave values
(diamonds) calculated by
Nussbaumer and
Storey (1980).
 (E) and
(E) and
 (T) for
interpolation and extrapolation in a compact form for the different
types of transitions.
(T) for
interpolation and extrapolation in a compact form for the different
types of transitions.