


3.1. Mass Constraints
Direct measurements of neutrino masses have given only upper limits
(see also the chapter by Robertson and Wilkerson). A secure upper
limit on the electron neutrino mass is roughly 15 eV. The Particle
Data Group [23]
notes that a more precise limit cannot be
given since unexplained effects have resulted in significantly
negative measurements of
m( e)2 in
tritium beta decay
experiments. However, this problem is at least partially resolved,
and the latest experimental upper limits on the electron neutrino mass
are 2.8 eV from the Mainz
[24]
and 2.5 eV from the Troitsk
[25]
tritium beta decay experiments (both 95% C.L.). There
is an upper limit on an effective Majorana neutrino mass of ~ 1
eV from neutrinoless double beta decay experiments
[26].
The upper limits from accelerator experiments on the masses of the
other neutrinos are
m(
e)2 in
tritium beta decay
experiments. However, this problem is at least partially resolved,
and the latest experimental upper limits on the electron neutrino mass
are 2.8 eV from the Mainz
[24]
and 2.5 eV from the Troitsk
[25]
tritium beta decay experiments (both 95% C.L.). There
is an upper limit on an effective Majorana neutrino mass of ~ 1
eV from neutrinoless double beta decay experiments
[26].
The upper limits from accelerator experiments on the masses of the
other neutrinos are
m( µ)< 0.17 MeV
(90% CL) and
m(
µ)< 0.17 MeV
(90% CL) and
m(
 ) < 18 MeV (95% CL)
[23,
27], but since stable
neutrinos with such large masses would certainly ``overclose the
universe'' (i.e., contribute such a large cosmological density that
the universe could never have attained its present age), cosmology
implies a much lower upper limit on these neutrino masses.
) < 18 MeV (95% CL)
[23,
27], but since stable
neutrinos with such large masses would certainly ``overclose the
universe'' (i.e., contribute such a large cosmological density that
the universe could never have attained its present age), cosmology
implies a much lower upper limit on these neutrino masses.
Before going further, it will be necessary to discuss the thermal
history of neutrinos in the standard hot big bang cosmology in order
to derive the corresponding constraints on their mass.
Left-handed neutrinos of mass
 1 MeV remain in thermal
equilibrium until the temperature drops to
T
1 MeV remain in thermal
equilibrium until the temperature drops to
T d, at which point
their mean free path first exceeds the horizon size and they
essentially cease interacting thereafter, except gravitationally
[28].
Their mean free path is, in natural units
(
d, at which point
their mean free path first exceeds the horizon size and they
essentially cease interacting thereafter, except gravitationally
[28].
Their mean free path is, in natural units
( = c = 1),
= c = 1),

 ~
[
~
[
 ne±]-1 ~
[(G2F
T2) (T3)]-1, where
GF
ne±]-1 ~
[(G2F
T2) (T3)]-1, where
GF
 10-5
GeV-2 is the Fermi
constant that measures the strength of the weak interactions. The
horizon size is
10-5
GeV-2 is the Fermi
constant that measures the strength of the weak interactions. The
horizon size is
 h ~
(G
h ~
(G  )-1/2 ~
MPl T-2,
where the Planck mass MP l
)-1/2 ~
MPl T-2,
where the Planck mass MP l
 G-1/2 = 1.22 x
1019 GeV. Thus
G-1/2 = 1.22 x
1019 GeV. Thus
 h /
h /

 ~ (T /
T
~ (T /
T d)3, with
the neutrino decoupling temperature
d)3, with
the neutrino decoupling temperature
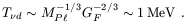
| (1) |
After T drops below 1/2 MeV,
e+e- annihilation ceases
to be balanced by pair creation, and the entropy of the
e+e- pairs heats the photons.
Above 1 MeV, the number density
n i of each left-handed
neutrino species and its right-handed antiparticle is
equal to that of the photons,
n
i of each left-handed
neutrino species and its right-handed antiparticle is
equal to that of the photons,
n ,
times the factor 3/4 from Fermi versus Bose statistics. But then
e+e- annihilation increases the
photon number density relative
to that of the neutrinos by a factor of 11/4.
(1)
As a result, the neutrino temperature
T
,
times the factor 3/4 from Fermi versus Bose statistics. But then
e+e- annihilation increases the
photon number density relative
to that of the neutrinos by a factor of 11/4.
(1)
As a result, the neutrino temperature
T , 0 =
(4/11)1/3
T
, 0 =
(4/11)1/3
T , 0.
Thus today, for each species,
, 0.
Thus today, for each species,
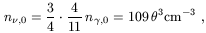
| (2) |
where 
 (T0 / 2.7 K).
With the cosmic background radiation temperature T0 =
2.728 ± 0.004 K
measured by the FIRAS instrument on the COBE satellite
[29].,
T
(T0 / 2.7 K).
With the cosmic background radiation temperature T0 =
2.728 ± 0.004 K
measured by the FIRAS instrument on the COBE satellite
[29].,
T , 0 = 1.947 K and
n
, 0 = 1.947 K and
n , 0 = 112
cm-3.
, 0 = 112
cm-3.
Since the present cosmological matter density is
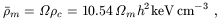
| (3) |
it follows that
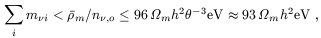
| (4) |
where the sum runs over all neutrino species with
M i
i
 1 MeV. (Heavier
neutrinos will be discussed in the next paragraph.)
Observational data imply that
1 MeV. (Heavier
neutrinos will be discussed in the next paragraph.)
Observational data imply that
 m
h2
m
h2
 0.1-0.3, since
0.1-0.3, since
 m
m
 0.3-0.5 and h
0.3-0.5 and h
 0.65 ± 0.1
[17].
Thus if all the dark matter were light neutrinos, the sum of their
masses would be
0.65 ± 0.1
[17].
Thus if all the dark matter were light neutrinos, the sum of their
masses would be  9-28 eV.
9-28 eV.
In deriving eq. (4), we have been assuming that all the
neutrino species are light enough to still be relativistic
at decoupling, i.e. lighter than an MeV. The bound (4)
shows that they must then be much lighter than that. In the
alternative case that a neutrino species is nonrelativistic
at decoupling, it has been shown
[30,
31,
32,
33,
34]
that its mass must then exceed several GeV, which is not
true of the known neutrinos
( e,
e,
 µ, and
µ, and

 ). (One might at first think that the Boltzmann factor
would sufficiently suppress the number density of
neutrinos weighing a few tens of MeV to allow compatibility with
the present density of the universe. It is the fact that they
``freeze out'' of equilibrium well before the temperature drops to
their mass that leads to the higher mass limit.)
We have also been assuming that the neutrino
chemical potential is negligible, i.e. that
| n
). (One might at first think that the Boltzmann factor
would sufficiently suppress the number density of
neutrinos weighing a few tens of MeV to allow compatibility with
the present density of the universe. It is the fact that they
``freeze out'' of equilibrium well before the temperature drops to
their mass that leads to the higher mass limit.)
We have also been assuming that the neutrino
chemical potential is negligible, i.e. that
| n -
n
-
n | <<
n
| <<
n .
This is very plausible, since the net baryon number density
(nb -
n
.
This is very plausible, since the net baryon number density
(nb -
n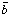 )
)
 10-9
n
10-9
n ,
and big bang nucleosynthesis restricts the allowed parameters
35]
(see also the chapter by Fuller).
,
and big bang nucleosynthesis restricts the allowed parameters
35]
(see also the chapter by Fuller).
1 In
the argument giving the 11/4 factor,
the key ingredient is that the entropy in
interacting particles in a comoving volume SI is conserved
during ordinary Hubble expansion, even during a process such
as electron-positron annihilation, so long as it occurs in
equilibrium. That is, SI =
gI(T)
N
 (T) = constant, where
N
(T) = constant, where
N = n
= n V is the number of photons in a given
comoving volume V, and gI =
(gB + 7/8 gF)I is the
effective number of helicity states in interacting particles
(with the factor of 7/8 reflecting the difference in
energy density for fermions versus bosons). Just above the
temperature of electron-positron annihilation,
gI =
g
V is the number of photons in a given
comoving volume V, and gI =
(gB + 7/8 gF)I is the
effective number of helicity states in interacting particles
(with the factor of 7/8 reflecting the difference in
energy density for fermions versus bosons). Just above the
temperature of electron-positron annihilation,
gI =
g + 7/8 x ge = 2 + 7/8 x 4 = 11/2; while below it,
gI =
g
+ 7/8 x ge = 2 + 7/8 x 4 = 11/2; while below it,
gI =
g = 2. Thus, as a result of the entropy of the
electrons and positrons being dumped into the photon gas at
annihilation, the photon number density is thereafter
increased relative to that of the neutrinos by a factor of
11/4.)
Back.
= 2. Thus, as a result of the entropy of the
electrons and positrons being dumped into the photon gas at
annihilation, the photon number density is thereafter
increased relative to that of the neutrinos by a factor of
11/4.)
Back.