3.2. Phase Space Constraint

We have just seen that light neutrinos must satisfy an upper bound on the sum of their masses. But now we will discuss a lower bound on neutrino mass that arises because they must be rather massive to form the dark matter in galaxies, since their phase space density is limited by the Pauli exclusion principle. A slightly stronger bound follows from the fact that they were not degenerate in the early universe.

The phase space constraint [36] follows from Jeans's theorem in classical mechanics to the effect that the maximum 6-dimensional phase space density cannot increase as a system of collisionless particles evolves. At early times, before density inhomogenitites become nonlinear, the neutrino phase space density is given by the Fermi-Dirac distribution

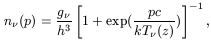
(5)

where here h is Planck's constant and g = 2 for each species of left-handed plus right-handed . Since momentum and temperature both scale as redshift z as the universe expands, this distribution remains valid after neutrinos drop out of thermal equilibrium at ~ 1 MeV, and even into the nonrelativistic regime T < m [28]. The standard version of the phase space constraint follows from demanding that the central phase space density 9[2 (2)^5/2 G r_c² m⁴]^-1 of the DM halo, assumed to be an isothermal sphere of core radius r_c and one-dimensional velocity dispersion , not exceed the maximum value of the initial phase space density n(0) = g / 2h³. The result is

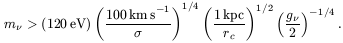
(6)

The strongest lower limits on m follow from applying this to the smallest galaxies. Both theoretical arguments regarding the dwarf spheroidal (dS) satellite galaxies of the Milky Way [37] and data on Draco, Carina, and Ursa Minor made it clear some time ago that dark matter dominates the gravitational potential of these dS galaxies, and the case has only strengthened with time [38]. The phase space constraint then sets a lower limit [39] m > 500 eV, which is completely incompatible with the cosmological constraint eq. (4). However, this argument only excludes neutrinos as the DM in certain small galaxies; it remains possible that the DM in these galaxies is (say) baryonic, while that in larger galaxies such as our own is (at least partly) light neutrinos. A more conservative phase space constraint was obtained for the Draco and Ursa Minor dwarf spheroidals [40], but the authors concluded that neutrinos consistent with the cosmological upper bound on m cannot be the DM in these galaxies. A similar analysis applied to the gas-rich low-rotation-velocity dwarf irregular galaxy DDO 154 [41] gave a limit m > 94 eV, again inconsistent with the cosmological upper bound.