4. COLD PLUS HOT DARK MATTER AND STRUCTURE FORMATION: _m = 1

Even if most of the dark matter is of the cold variety, a little hot dark matter can have a dramatic effect on the predicted distribution of galaxies. In the early universe, the free streaming of the fast-moving neutrinos washes out any inhomogeneities in their spatial distribution on the scales that will later become galaxies. If these neutrinos are a significant fraction of the total mass of the universe, then although the density inhomogeneities will be preserved in the cold dark matter, their growth rates will be slowed. As a result, the amplitude of the galaxy-scale inhomogeneities today is less with a little hot dark matter than if the dark matter is only cold. (With the tilt n of the primordial spectrum P_p(k) = A kⁿ fixed - which as we discuss below is not necessarily reasonable - the fractional reduction in the power on small scales is P / P 8 / _m [58]. See Fig. 1 for examples of how the power spectrum P(k) is affected by the addition of hot dark matter in _m = 0.4 flat cosmologies.) Since the main problem with _m = 1 cosmologies containing only cold dark matter is that the amplitude of the galaxy-scale inhomogeneities is too large compared to those on larger scales, the presence of a little hot dark matter appeared to be possibly just what was needed. And, as was mentioned at the outset, a CHDM model with _m = 1, = 0.2, and Hubble parameter h = 0.5 is perhaps the best fit to the galaxy distribution in the nearby universe of any cosmological model. The effects of the relatively small amount of hot dark matter in a CHDM model on the distribution of matter compared to a purely CDM model are shown graphically in [59]; cf. also [60]. As expected, within galaxy halos the distribution of cold and hot particles is similar. But the hot particles are more widely distributed on larger scales, and the hot/cold ratio is significantly enhanced in low-density regions.

The first step in working out the theory of structure formation is to use linear perturbation theory, which is valid since cosmic microwave background measurements show that density fluctuations are small at the redshift of recombination, z_r ~ 10³. The most extensive early calculations of this sort were carried out by Holtzman [61, 62], who concluded that the most promising cosmological models were CHDM and CDM [63]. The most efficient method of computing the linear evolution of fluctuations now is that used in the CMBFAST code [64]. An alternative Monte Carlo treatment of the evolution of neutrino density fluctuations was given by [65], but the differences from the usual treatment appear to be small. Detailed analytic results have been given by [66, 67] and reviewed in [60]. But the key point can be understood simply: there is less structure in CHDM models on small scales because the growth rate of cold dark matter fluctuations is reduced on the scales where free streaming has wiped out neutrino fluctuations. Let us define the fluctuation growth rate f by

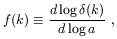
(9)

where (k) is the amplitude of the fluctuations of wave number k = 2 / in cold dark matter, and as usual a = 1 / (1 + z) is the scale factor. For _m = 1 CDM fluctuations, the growth rate f = 1. This is also true for fluctuations in CHDM, for k sufficiently small that free-streaming has not significantly decreased the amplitude of neutrino fluctuations. However, in the opposite limit k -> [43, 60],

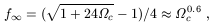
(10)

assuming that _c + = 1. For example, for = 0.2, f = 0.87. Even though the growth rate is only a little lower for these large-k (i.e., short-wavelength) modes, the result is that their amplitude is decreased substantially compared to longer-wavelength modes.

The next step in determining the implications for structure formation is to work out the effects on nonlinear scales using N-body simulations. This is harder for Cold+Hot models than for CDM because the higher velocities of the neutrinos require more particles to adequately sample the neutrino phase space. The simulations must reflect the fact that the neutrinos initially have a redshifted Fermi-Dirac phase space distribution [68]. These CHDM simulations were compared with observational data using various statistics. CHDM with = 0.3, the value indicated by approximate analyses [63, 69], was shown to lead to groups of galaxies having substantially lower velocity dispersions than CDM, and in better agreement with observations [70]. But it also leads to a Void Probability Function (VPF) with more intermediate-sized voids than are observed [71]. This theory had so little small-scale power that a quasi-linear analysis using the Press-Schechter approximation showed that there would not be enough of the high-column-density hydrogen clouds at high redshift z ~ 3 known as damped Lyman- systems [72, 73, 74]. But CHDM with = 0.2 suppresses small-scale fluctuations less and therefore has a better chance of avoiding this problem [75]. Simulations [76] showed that this version of CHDM also has a VPF in good agreement with observations [77]. The group velocity dispersions also remained sufficiently small to plausibly agree with observations, but it had become clear that the N-body simulations used lacked sufficient resolution to identify galaxies so that this statistic could be measured reliably [78].

A resolution problem also arose regarding the high-redshift damped Lyman- systems. Earlier research had been based on the idea that these systems are rather large disk galaxies in massive halos [79], but then high-resolution hydrodynamical simulations [80] showed that relatively small gaseous protogalaxies moving in smaller halos provide a good match to the new, detailed kinematic data [81]. It thus appeared possible that CHDM models with 0.2 might produce enough damped Lyman- systems. With the low Hubble parameter h ~ 0.5 required for such _m = 1 models, the total neutrino mass would then be 5 eV.

While neutrino oscillation experiments can determine the differences of squared neutrino masses, as we will briefly review next, cosmology is sensitive to the actual values of the neutrino masses - for any that are larger than about 1 eV. In that case, cosmology can help to fill in the neutrino mass matrix.

One example of this is the fact that if the hot DM mass is roughly evenly shared between two or three neutrino species, the neutrinos will be lighter than if the same mass were all in one species, so that the free streaming length will be longer. A consequence is that, for the same total neutrino mass and corresponding , the power spectrum will be approximately 20% lower on the scale of galaxy clusters if the mass is shared between two neutrino species [1]. Since the amplitude and ``tilt'' n of the power spectrum in CDM-type models is usually fixed by comparison with COBE and cluster abundance, this has the further consequence that higher n (i.e., less tilt) is required when the neutrino mass is divided between comparable-mass neutrino species. Less tilt means that there will be more power on small scales, which appeared to be favorable for the CHDM model, for example because it eased the problems with damped Lyman- systems [1, 82].