Copyright © 1993 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
653-703 Copyright © 1993 by Annual Reviews. All rights reserved |
Over the last decade the anisotropy of the microwave background
radiation has emerged as a field of fundamental importance to
astrophysics due to its significance in theories of galaxy formation
and in the quest for the physical origin of fluctuations. The history
of the development of this subject may be divided into three phases:
In the first phase, lasting up until about 1982, searches for
anisotropy were carried out on angular scales ranging from two arc
minutes to 180°, and, apart from the dipole term due to the
peculiar velocity of the earth relative to the Hubble flow (eg.
Fixsen et al 1983,
Lubin et al 1985,
Halpern et al 1985,
Strukov & Skulachev
1988,
Meyer et al 1991b,
Smoot et al 1991b),
no anisotropies were
detected down to the level of  T/T
T/T  10-4 - 10-3 expected from simple scenarios for
galaxy formation. In the
second phase, from ~ 1983 to ~ 1989, sensitivities were
improved by a full order of magnitude, but still no intrinsic
anisotropies were detected. Over the same period many theoretical
models were eliminated and new models were explored which predicted
fractional anisotropies approaching 10-6. We are presently in
the third phase: Sensitivities on all angular scales have reached
levels where confusing signals due to discrete sources or diffuse
Galactic emission - due to dust, free free emission and synchrotron
radiation - dominate the signals and have to be removed before the
intrinsic anisotropy can be studied.
10-4 - 10-3 expected from simple scenarios for
galaxy formation. In the
second phase, from ~ 1983 to ~ 1989, sensitivities were
improved by a full order of magnitude, but still no intrinsic
anisotropies were detected. Over the same period many theoretical
models were eliminated and new models were explored which predicted
fractional anisotropies approaching 10-6. We are presently in
the third phase: Sensitivities on all angular scales have reached
levels where confusing signals due to discrete sources or diffuse
Galactic emission - due to dust, free free emission and synchrotron
radiation - dominate the signals and have to be removed before the
intrinsic anisotropy can be studied.
There are excellent reviews of the first phase (Weiss 1980, Partridge 1980, Wilkinson 1982, Partridge 1983) and portions of the second phase (Wilkinson 1986, Partridge 1987, Partridge 1988). In addition to thorough discussions of the observations, two of these reviews (Weiss 1980, Partridge 1988) give extensive accounts of the instrumentation and observing techniques which have been most effective in this field. In this article we attempt a comprehensive review of the observations in the second and third phases and we discuss the confusing signals which have begun to complicate the interpretation of observations. We also discuss the prospects for overcoming these difficulties. We do not discuss theories of galaxy formation and the generation of anisotropy in the microwave background radiation or other cosmological implications of the observations since these are scheduled to be reviewed in a subsequent volume in this series.
It is useful to keep in mind the mass scales that are probed by
observations of the anisotropy of the microwave background radiation
on different angular scales. If we assume that the microwave
background radiation was last scattered at a redshift z >> 1, when
the density fluctuations 
 /
/  >> 1, then the mass,
M, of a sphere at the last scattering surface which subtends
angular diameter
>> 1, then the mass,
M, of a sphere at the last scattering surface which subtends
angular diameter 
 , calculated from the
Robertson-Walker metric for a standard Friedmann cosmology
(eg.
Weinberg 1972)
is given by the relation:
, calculated from the
Robertson-Walker metric for a standard Friedmann cosmology
(eg.
Weinberg 1972)
is given by the relation:
where
The range of angular scales 1-20° may have particular significance for
anisotropy of the microwave background radiation since the horizon
scale at z >> 1 subtends an angle:
Thus, if the last scattering surface of the microwave background
radiation was at a redshift z
In order to interpret observations of the microwave background radiation,
it is necessary to assume some form for the distribution on the sky of
the intrinsic fluctuations. This immediately raises problems because
of our ignorance concerning the form of this distribution. A complete
description of the fluctuations in
In this review we will consider fluctuations in the temperature of the
microwave background radiation only on angular scales up to
20°. We do not discuss the quadrupole and dipole terms here
because the COBE satellite
(Smoot et al 1991a,
b)
has obtained by
far the best data to date on these scales and the situation is likely
to change substantially before this review is published. While the
same may be true for observations down to ~ 7°, the COBE
resolution limit, we do consider observations in the range
1-20° and thus cover the region of overlap between
COBE and small angular scale anisotropy measurements. We consider the
two-dimensional correlation function, C, for the temperature pattern
on the celestial sphere. We assume that C has circular symmetry and
may therefore be expressed in terms of a single variable,
where F(k) is a filter function which depends upon the
shape of the antenna beam and the sampling scheme on the sky. In general a
Gaussian beam is a good approximation to the response of the antenna.
The resulting filter functions for such a beam and for single-beam,
single switched and double-switched sampling on the sky are given in
Table 1. According to Equation 3 we see that, as
previously stated, in order
to interpret observed values of, or limits on, < (
For the purposes of this review, we assume that the mean temperature
of the microwave background radiation is T = 2.735 K, as measured by
Mather et al (1990)
with the COBE satellite, and,
wherever possible, we have adjusted published values of
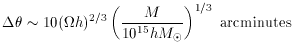
 is the density parameter, and
the Hubble constant H = 100 h km s-1
Mpc-1.
is the density parameter, and
the Hubble constant H = 100 h km s-1
Mpc-1.
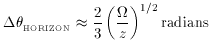
 1500, the horizon size at last
scattering subtends an angle
1500, the horizon size at last
scattering subtends an angle 
 HORIZON
HORIZON  1°. However if the last scattering surface was at z
1°. However if the last scattering surface was at z  40
then
40
then 
 HORIZON
HORIZON
 6°. For
cosmological models with early reionization, primordial intrinsic
fluctuations could be erased up to the horizon angular scale,
i.e. up to, at most, angular scales of
6°. For
cosmological models with early reionization, primordial intrinsic
fluctuations could be erased up to the horizon angular scale,
i.e. up to, at most, angular scales of  6°.
Reionization at z < 40 would not completely erase primordial intrinsic
fluctuations up to this scale because the density of matter at later
epochs is too low to give high optical depths on a Hubble length even
if all the intergalactic material is fully ionized.
6°.
Reionization at z < 40 would not completely erase primordial intrinsic
fluctuations up to this scale because the density of matter at later
epochs is too low to give high optical depths on a Hubble length even
if all the intergalactic material is fully ionized.
 T comprises both the
distribution in amplitude (as can be obtained from a histogram of
T comprises both the
distribution in amplitude (as can be obtained from a histogram of
 T measurements obtained from
binning the sky into small
pixels), and the spatial distribution (as represented by the spatial
autocorrelation function or, alternatively, the power spectrum, W,
of
T measurements obtained from
binning the sky into small
pixels), and the spatial distribution (as represented by the spatial
autocorrelation function or, alternatively, the power spectrum, W,
of  T). In general the
spatial distribution does not uniquely
determine the amplitude distribution but in the case of a Gaussian
spectrum, W, the amplitude distribution is completely
determined. This property of a Gaussian random field - that the
statistical properties are fully specified by the two-point
correlation function - makes it easy to compare observations with
Gaussian models. The spectrum of the sky cannot be truly Gaussian
because the sky is finite, however at small angular scales models or
scenarios have been proposed for which the amplitude distribution is
Gaussian and the spectrum is approximately Gaussian (e.g.
Bond & Efstathiou 1987).
Models have also been proposed in which both the
amplitude distribution and the power spectrum are strongly
non-Gaussian. (e.g.
Ikeuchi 1981,
Ostriker & Cowie 1981,
Ostriker et al 1986,
Ostriker & Thompson 1987,
Kofman & Pogosyan 1988,
Salopek et al 1989).
T). In general the
spatial distribution does not uniquely
determine the amplitude distribution but in the case of a Gaussian
spectrum, W, the amplitude distribution is completely
determined. This property of a Gaussian random field - that the
statistical properties are fully specified by the two-point
correlation function - makes it easy to compare observations with
Gaussian models. The spectrum of the sky cannot be truly Gaussian
because the sky is finite, however at small angular scales models or
scenarios have been proposed for which the amplitude distribution is
Gaussian and the spectrum is approximately Gaussian (e.g.
Bond & Efstathiou 1987).
Models have also been proposed in which both the
amplitude distribution and the power spectrum are strongly
non-Gaussian. (e.g.
Ikeuchi 1981,
Ostriker & Cowie 1981,
Ostriker et al 1986,
Ostriker & Thompson 1987,
Kofman & Pogosyan 1988,
Salopek et al 1989).
 .
Thus C(
.
Thus C( ) = < T(
) = < T(
 1) T(
1) T( 2) >,
where
2) >,
where 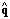 1
·
1
·
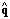 2 = cos
2 = cos  . In the small angle
approximation the power spectrum, W, of the fluctuations may then be
expressed in terms of the single wavenumber variable, k, such that
C(
. In the small angle
approximation the power spectrum, W, of the fluctuations may then be
expressed in terms of the single wavenumber variable, k, such that
C( ) and W(k) form a Hankel
transform pair. The expected
variance of the data can then be written
) and W(k) form a Hankel
transform pair. The expected
variance of the data can then be written
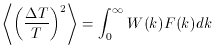
 T/T)2 > in terms
of the limits these place on the sky
fluctuations we need to assume some form for W(k).
T/T)2 > in terms
of the limits these place on the sky
fluctuations we need to assume some form for W(k).
 T/T
to conform with this value.
T/T
to conform with this value.
Switching scheme
Filter function
Gaussian beam, no switching
k/2  e-k2
e-k2 02
02
Single switching, beam separation  s
s
k/2  e-k2
e-k2 02 (1 - J0
(k
02 (1 - J0
(k s))
s))
Double switching
 e-k2
e-k2 02 (3/2 - 2J0
(k
02 (3/2 - 2J0
(k s) + 1/2
J0 (2k
s) + 1/2
J0 (2k s))
s))