Annu. Rev. Astron. Astrophys. 1992. 30: 653-703 Copyright © 1993 by Annual Reviews. All rights reserved

3. OBSERVATIONS

In the absence of any proven theory for the origin and evolution of structure it is important that searches for possible anisotropy be carried out on all angular scales. Sensitive searches have therefore been made with a wide variety of techniques from angular scales of arc seconds to tens of degrees. We discuss below separately observations on scales < 1', on scales of 1'-1°, and on scales of 1-20°.

3.1 Observations on Angular Scales < 1'

3.1.1 VLA OBSERVATIONS The most sensitive searches for microwave background radiation anisotropy at angular scales < 1' have been carried out on the VLA. During the 1980's five different anisotropy studies were carried out (Fomalont et al 1984, Knoke et al 1984, Martin & Partridge 1988, Fomalont et al 1988, Hogan & Partridge 1989). Aperture synthesis observations offer some significant advantages over filled aperture observations in searches for anisotropy since (a) in filled aperture work almost any systematic source of noise mimics a true sky signal, and such noise signals have to be discriminated against by switching schemes which complicate the interpretation of the observations and generally prohibit the making of real sky images; and (b) atmospheric effects are a dominant source of systematic noise for most filled aperture ground-based observations. Aperture synthesis observations overcome these difficulties to a large extent because interferometry eliminates uncorrelated signals and signals which fill a large fraction of the primary beam - such as those caused by ground spillover, and atmospheric effects appear primarily as an added component of random noise over the whole map. Perhaps the greatest advantage afforded by interferometric observations over single dish observations is the elimination of slowly varying effects - i.e. the low-frequency component of noise which is always present in radio astronomical observations.

However, aperture synthesis observations have their own peculiar problems, the most severe of which are antenna shadowing and cross-talk and systematic offsets in the correlator. Such problems severely affected some of these studies (Fomalont et al 1984, Knoke et al 1984) but were significantly reduced or eliminated in the later work (Martin & Partridge 1988, Fomalont et al 1988, Hogan & Partridge 1989). A further difficulty which besets all high resolution observations, and which causes problems at the VLA especially in observations at frequencies below ~ 10 GHz, is that due to confusion by discrete sources. All of the VLA studies with the exception of that carried out at 14.9 GHz by Hogan & Partridge (1989) were made at 4.9 GHz, and were, therefore, dominated by discrete sources.

In spite of these difficulties, impressive limits have been placed on anisotropy of the microwave background radiation on sub-arc minute scales. These limits are summarized in Table 2.

Table 2. 95% upper limits on T/T at angular scales < 1'

Experiment	Angular Scale	T/T x 105	Comments
Fomalont et al. 1984	18" 30" 60"	95 80 50	4.9 GHz; monochromatic W(k) monochromatic W(k) monochromatic W(k)
Knobe et al. 1984	6" 12" 18"	320 170 120	4.9 GHz; Gaussian W(k) Gaussian W(k) Gaussian W(k)
Martin & Partridge	18"-160"	40	4.9 GHz; monochromatic W(k)
Fomalont et al. 1988	12" 18" 30" 60"	85 12 8 6	4.9 GHz; monochromatic W(k) monochromatic W(k) monochromatic W(k) monochromatic W(k)
Hogan & Partridge	5".4-48" 10"-48" 18"-50"	63 32 16	14.9 GHz; monochromatic W(k) monochromatic W(k) monochromatic W(k)
Kreysa & Chini	30"	26	230 GHz; monochromatic W(k); LR test.

In all of the 4.9 GHz observations excess variance was observed. In the work of Fomalont et al (1984) and Knoke et al (1984) the excess was interpreted in terms of discrete sources, but in their study Martin and Partridge (1988), after a careful analysis of the expected level of contribution from discrete sources, based on 20 cm source counts (Mitchell & Condon 1985), concluded that it was unlikely that the excess signal was entirely due to discrete sources.

The most detailed treatment of the effects of discrete sources is that of Fomalont et al (1988). In an elegantly designed series of observations in 1987 they observed a single field for 10 hours a day on each of five consecutive days and they then analyzed the first 2.5 days and the remaining 2.5 days separately. From the resulting two images they then formed the sum image and the difference image. The sum image provided the most sensitive measure of the actual sky variations while the difference image provided a very useful measure of all of the various noise terms apart from actual sky signals. To take account of the effects of discrete sources they carried out a Monte Carlo analysis which mimicked their observations including the effects of the missing zero spacings in the VLA data. They assumed a variety of power laws for the number-flux density differential counts of the form:

(7)

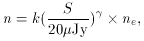
where n is the number of sources per steradian per Jansky and flux density S, and n_e is the static Euclidean count of 90S^2.5 sources sr^-1 Jy^-1. Hence, by fitting the simulations to the overall variance, ², and to the variance of the intensities greater than the average, ²₊, and the variance of the intensities less than the average, ²_-, they determined the acceptable limits on and k. Their best-fitting model has = 1.0 and k = 0.0058. An important result of these simulations was that the observed increase in the ²_- near the center of the field is found to be due to the effects of missing spatial frequencies and discrete sources. This provides a convincing explanation of the excess variance discussed by Kellermann et al (1986) and by Martin & Partridge (1988). The upper limits on anisotropy derived by Fomalont et al (1988) are therefore the best understood and the most stringent limits on the anisotropy on angular scales less than one arc minute. In the following section we combine these results with more recent observations by Partridge (private communication) and results from the Owens Valley Radio Observatory and from the South Pole to derive upper limits on the anisotropy over the interval from 0.1-100', over which a Gaussian distribution is a reasonable approximation, to some of the more favored models of galaxy formation.

3.1.2 IRAM OBSERVATIONS Kreysa & Chini (1989) observed 25 known quasars at 230 GHz with the 30 meter IRAM telescope (resolution 30"). Only four quasars were detected and the data from the empty fields were used to set limits on the microwave background anisotropy. Their results, using the likelihood ratio technique, are given in Table 2. These results are of importance for the limits they set on fluctuations in dust emission (Bond et al 1991).