Copyright © 1993 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
653-703 Copyright © 1993 by Annual Reviews. All rights reserved |
4.2 Confusion by Galactic Synchrotron Emission
The group at the University of Durham has carried out a detailed study of the implications of Galactic synchrotron emission for microwave background radiation observations (Lawson et al 1987, Banday et al 1991, Banday & Wolfendale 1991). Similar studies have been carried out independently by Lasenby et al (1991) and us (in preparation). All of these studies indicate clearly that at frequencies below ~ 15 GHz fluctuations in the diffuse Galactic synchrotron emission are expected at the level of the anisotropy detected by Davies et al (1987), and that this anisotropy could be mainly due to the Galaxy and not to fluctuations in the microwave background radiation. We discuss here the published work by the Durham group. The methods used by the three separate groups were very similar and were based on the same low frequency radio surveys.
The main problem in this area is that there are no accurately
calibrated extensive sky surveys at frequencies above 1420 MHz. The
dependance of the intensity of the Galactic synchrotron emission,
I( )Gse upon
frequency may be approximated by a power law over
a fairly wide range in frequency - i.e. I(
)Gse upon
frequency may be approximated by a power law over
a fairly wide range in frequency - i.e. I( )Gse =
I(
)Gse =
I( 0)Gse x (
0)Gse x ( /
/  0)
0) , where
, where  lies
between -0.5 and -1.1. It is well-known that the
power law steepens at high frequencies. The microwave background
radiation, on the other hand, is known to follow a Planck black-body
curve to within the precision of the COBE measurements (Mather et al
1990). The ratio of the intensities of these two emission processes
is, therefore, a strong function of frequency:
lies
between -0.5 and -1.1. It is well-known that the
power law steepens at high frequencies. The microwave background
radiation, on the other hand, is known to follow a Planck black-body
curve to within the precision of the COBE measurements (Mather et al
1990). The ratio of the intensities of these two emission processes
is, therefore, a strong function of frequency:
The drop in intensity of the Galactic synchrotron emission with
increasing frequency makes it far more difficult to measure accurately
the Galactic synchrotron emission at high frequencies than at low
frequencies. For this reason, and because of the more complex
instrumentation required, the 19 GHz balloon surveys discussed above
are not sufficiently sensitive to detect Galactic emission away from
the plane. To estimate the Galactic synchrotron emission at 10 GHz
and above, one therefore has to rely upon extrapolation from low
frequencies and this introduces significant uncertainties in the
predicted levels of synchrotron radiation.
Lawson et al (1987)
used many of the published maps of large regions of the
sky at frequencies between 38 MHz and 1420 MHz to determine the
variations in spectral index of the Galactic synchrotron emission over
the sky and over this range of frequencies. Their detailed analyses
and spectral index maps indicate that the best surveys for the purpose
of estimating the Galactic synchrotron emission as a function of
frequency are those at 408 MHz by Haslam and his co-workers
(Haslam et al 1970,
1974,
1981);
and at 1420 MHz by
Reich (1982) and by
Reich and Reich (1986).
Banday et al (1991) and
Banday and Wolfendale
(1991)
have used these
observations in an attempt to predict the expected level of Galactic
synchrotron emission at the frequency of the
Davies et al (1987)
observations and with the same experimental setup as used by these authors.
They carried out a number of simulations which reproduce fluctuations
at the same level as those observed by Davies et al, but do not
reproduce the observed fluctuations in detail. The predicted level of
anisotropy due to the Galactic synchrotron emission in a
double-differencing experiment is shown in
Figure 6, together with the
signal at 10.46 GHz measured by
Davies et al (1987).
Lasenby et al (1991)
have carried out similar simulations, with the
same results. An example of one particular simulation by Lasenby
(private communication) is shown in
Figure 5. Also shown is a running
Gaussian mean of the Davies et al data. It is clear that Galactic
synchrotron emission can account for fluctuations of the level
observed by Davies et al, but that there is not good agreement
in detail. The lack of good agreement in detail is not surprising
since it is well known that the index
This result by
Davies et al (1987)
was the first convincing case in which the
sensitivity of the observations was limited by diffuse Galactic
synchrotron emission and it exemplifies the difficulties that now face
observers in this field. In order to account accurately for the
effects of foreground fluctuations, these must be not simply
detected but also measured with greater accuracy than the
level at which intrinsic fluctuations are being studied if they are to
be removed with the requisite precision. This raises the question of
whether it is reasonable to expect to be able to subtract out
foreground effects with the required accuracy.
The strong frequency dependance of the specific intensity of the
Galactic synchrotron emission compared with that of the microwave
background radiation, given by the relation in Equation 10, means
that multi-frequency observations can, in principle, be used to
subtract out the effects of the Galactic synchrotron emission.
Over the last two years we have been involved in a detailed study of
the contamination caused by the Galactic synchrotron emission (in
preparation). The 408 MHz
(Haslam et al 1970,
1974,
1981,
Lawson et al 1987)
and the 1420 MHz
(Reich 1982,
Reich & Reich 1986)
maps were kindly supplied to us by Banday. The resolution on these maps was
1°. We scaled the maps at these two frequencies by the same
factor, such that the extrapolation to ~ 30 GHz in the Galactic
plane is consistent with the COBE results
(Wright et al 1991).
The scaled maps then give the correct intensity and the level of
fluctuations at 26-40 GHz. We then selected 10 x 10° regions of sky
and searched for regions of this size in
which the fluctuations were a minimum. Over the whole sky we found
ten 10 x 10° patches for which the rms variations
due to synchrotron and dust emission were less than 9 µK.
Clearly, one can have no confidence about the details of the
synchrotron emission after extrapolating over this large range in
frequency, but this does give a reasonable estimate of the intensity
and fluctuations in intensity in this frequency range. We also added
in our best estimate of the contribution from the infrared cirrus
(from IRAS data scaled to fit the COBE results) which is
considerably lower in intensity than the synchrotron component at these
frequencies, and we included the microwave background radiation
contribution with the addition of a randomly varying component. We
then simulated the extraction of the microwave background radiation
signal from this ``fake sky'' data assuming different levels of random
noise. The results are shown in
Figure 7. As the instrumental noise
per channel goes to zero the error in extrapolation of the microwave
background radiation fluctuations approaches the level of fluctuations
in the dust model we have used (i.e. ~ 1.5 µK). We see
that, for example, fluctuations in the microwave background radiation
can be extracted with an accuracy of 1 µK if the noise in each
of the seven channels is 2 µK. Given only data in this
frequency range, it is not possible with achievable sensitivities, to
subtract out the contribution due to dust.
Based on this simulation, we are confident that if multi-frequency sky
maps could be made with rms noise per channel at about this level it
would be possible to subtract out the Galactic synchrotron emission
with enough precision to make a map of the intrinsic microwave
background radiation anisotropy with sensitivity 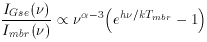

Figure 6. Levels predicted by
Banday et al (1991) of
 T/T due to Galactic
synchrotron emission as a function of
observing frequency, for double-switched observations. The circle
indicates the anisotropy detected by
Davies et al
(1987) at 10.4 GHz.
T/T due to Galactic
synchrotron emission as a function of
observing frequency, for double-switched observations. The circle
indicates the anisotropy detected by
Davies et al
(1987) at 10.4 GHz.
 varies with frequency,
and, with an extrapolation over such a wide range in frequency as
this, small variations in
varies with frequency,
and, with an extrapolation over such a wide range in frequency as
this, small variations in  ,
coupled with uncertainties in the
absolute levels of the low frequency observations and other systematic
effects, could easily account for the differences between observations
and predictions.
,
coupled with uncertainties in the
absolute levels of the low frequency observations and other systematic
effects, could easily account for the differences between observations
and predictions.
 T/T
T/T  10-6.
10-6.