Copyright © 1993 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1992. 30:
653-703 Copyright © 1993 by Annual Reviews. All rights reserved |
4.5 The Sunyaev-Zel'dovich Effect
The Sunyaev-Zel'dovich effect was last reviewed in these pages in 1980 (Sunyaev & Zel'dovich 1980a). At that time there were no convincing detections of the Sunyaev-Zel'dovich effect, although a number of claims had been made which were not substantiated by further observations, or by other groups. The maximum decrements at centimeter wavelengths due to the Sunyaev-Zel'dovich effect expected from rich clusters of galaxies lie in the range ~ 100-1000 µK. Successful observations of the Sunyaev-Zel'dovich effect therefore depend on observations with sensitivity ~ 20 µK. Thus the same systematic effects which plague observations of intrinsic anisotropy complicate observations of the Sunyaev-Zel'dovich effect - atmospheric emission, ground spillover, receiver gain variations, etc.
| Cluster |  ex a |  TRJ (mK)
b | T(0) (mk)
c
| References |
| 0016+16 | 1'.0 | Uson 1987 | ||
| Birkinshaw 1990 | ||||
| Abell 665 | 2'.0 | Uson 1987 | ||
| Birkinshaw 1990 | ||||
| Abell 2218 | 2'.1 | Uson 1985 | ||
| Birkinshaw 1990 | ||||
| a Angular size of X-ray core. | ||||
| b Rayleigh-Jeans decrement at observed frequency. | ||||
c Equivalent
decrement at  = 0.
| ||||
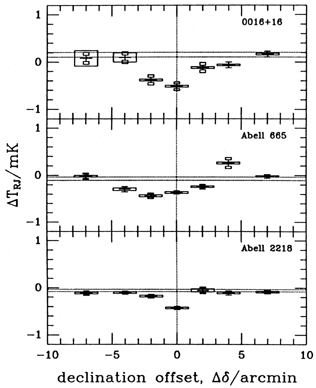
For the purposes of this review the Sunyaev-Zel'dovich effect is a foreground contamination, and we refer the interested reader to the reviews by Birkinshaw (1990, 1991) for more detailed accounts of the field. Birkinshaw (1991) lists all published attempts at Sunyaev-Zel'dovich effect measurements (see his Table 1). The results on the same clusters by different observers, and even of the same observers at different times, do not agree (see his Table 2). The most sensitive observations are those of Birkinshaw and his collaborators (Birkinshaw et al 1984, 1991, 1992; Birkinshaw 1990, 1991) and of Uson (1985, 1987). In their observations since 1984, the results from these two groups have been consistent on three rich clusters - 0016+16, Abell 665 and Abell 2218, as shown in Table 5. Birkinshaw's results for different offset positions in these three clusters are shown in Figure 8. It is clear that the Sunyaev-Zel'dovich effect has indeed been detected in these three clusters.
|
Figure 8. Results of observations of the Sunyaev
Zel'dovich effect in three clusters at 20 GHz by
Birkinshaw et al (1992).
The results are
plotted as a function of the offsets in declinations from the nominal
cluster centers. Crosses represent the data with ± 1 errors
deduced from the full dataset, with the widths of the crosses equal to
the FWHM of the OVRO 40 meter telescope beam. Thicker extensions to
the erorr bars indicate increases in the errors implied by
year-to-year discordance in the data. Boxes around each point
represent the maximum estimated systematic errors for each point, due
to uncertainties in confusion by discrete sources. The estimated
level of the local zero in each scan is indicated by the dotted lines,
which mark the ± 1 range
of Tzero. The peak
decrement in Abell 665 occurs 2 arcminutes south of the center
of the optical cluster, but coincides with the centroid of X-ray emission
(Birkinshaw et al 1991).
|
Bond and Myers
(1991a,
b)
have constructed a cold dark matter
model using a Monte Carlo hierarchical peak simulation method. This
gives them the three-dimensional distribution of galaxy clusters for
various values of the biassing parameter, b
. They point out
that clusters are rare events defined by the tail of a Gaussian
probability distribution so that the mass function for clusters is
very sensitive to the value of b. They adopt plausible cluster
parameters and hence calculate the X-ray emissivity of the clusters
and also the expected Sunyaev Zel'dovich effect from their
three-dimensional model. An example for the case of b = 1 is
shown in Figure 9. In this simulation the
Sunyaev Zel'dovich effect
map has been convolved with the 1'.8 beam of the 40 meter telescope
of the Owens Valley
Radio Observatory. For this map the average y-
parameter is 1 x 10-6, and in the Rayleigh-Jeans regime
=
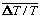-2
. The rms value of
T/T is 6.3 x
10-6, about a factor of two below the
present limits of isotropy observations, but well within the range of
the sensitivity levels that we are seeking. The corresponding values
for the map derived by Bond and Myers for b = 1.4 are
significantly lower than these.
|
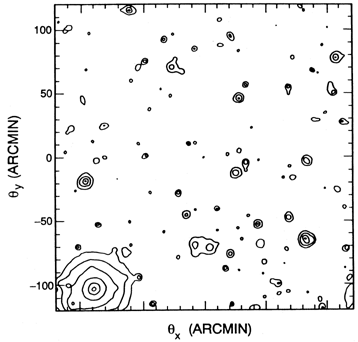
Figure 9. A simulated contour image, by
Bond and Myers (1991a),
of Sunyaev
Zel'dovich effect sources in the cold dark matter model with biassing
b
= 1. The original map has been convolved with a 1'.8
beam. The contour levels decrease by factors of two from the peak at
T = -5 x
10-6( B / 0.05).
|
It is clear from these observations and simulations that conditions in at least some clusters are responsible for significant distortions in the microwave background radiation, and that the Sunyaev-Zel'dovich effect is must be taken into account when searching for intrinsic anisotropy in the microwave background radiation.
There are many aspects of the Sunyaev-Zel'dovich effect which make it a useful tool in cosmological studies (e.g. Sunyaev & Zel'dovich 1980a, b, Birkinshaw et al 1991), but perhaps the most important from the point of view of the present review is that the detection of a decrement in the direction of distant clusters demonstrates directly and unequivocally that the microwave background radiation does indeed originate at high redshift.