


2.2. Stellar Disruption
An alternative possibility is that the gas is supplied by disrup-
tion of stars in the dense core around the central black hole.
Such processes as stellar collisions might occur in a dense
stellar system, even if there were not a central black hole
[1 -
4].
But one might ask: How does the presence of a massive
central black hole affect the surrounding stars? Several authors
[16 -
29]
have recently investigated some aspects of this
phenomenon, motivated by its possible relevance to globular
clusters or galactic nuclei. If the stellar distribution is
characterized by a "core radius" rc and a density of
nc, the virial theorem
then tells us that the characteristic velocity dispersion is
 c
c
 (Gm*ncrc2)1/2, m* being the typical stellar mass. The
presence of a central point mass Mh, such that
ncrc3m*
>> Mh >> m*,
produces an extra "r-1" potential well, which can
affect the stellar velocity field out to a distance rh
= (GMh / vc2).
(Gm*ncrc2)1/2, m* being the typical stellar mass. The
presence of a central point mass Mh, such that
ncrc3m*
>> Mh >> m*,
produces an extra "r-1" potential well, which can
affect the stellar velocity field out to a distance rh
= (GMh / vc2).
The effect on the density distribution is less straightforward. However, if the central mass has been present for a time compar- able with the stellar relaxation time (or "reference time") tR in the core, we expect some kind of stationary state to be established, involving a slow, inward drift of the stars. (In fact the whole core will evolve on a time scale ~ 10tR so the situation will never be an exactly stationary one.)
A central black hole provides an effective "sink" for stars
approaching too close to it - such stars will be swallowed or
disrupted. There is therefore no possibility of establishing an
"isothermal" distribution where the density n(r) rises
exponentially within rh. This point was first
emphasised by Peebles
[16]
in the context of globular clusters. He conjectured that
the distribution of stars in bound orbits followed a power law
N(E)  E-p in binding energy E. There is then a
power law cusp in the stellar density:
E-p in binding energy E. There is then a
power law cusp in the stellar density:
and the velocity dispersion within the cusp scales as r-1/2.
Insofar as the situation is controlled by stellar-dynamical
relaxation processes
[18,
19], and provided
there has been time
for a stationary state to be established, the value of q is ~ 7/4.
This is the value such that the rate at which energy is
"conducted" outward through the cusp
(
Apart from rs, the following two length-scales, which
depend on the physical properties of the stars, are relevant to the problem:
(i) The tidal radius (or "Roche radius") within which a star
would be disrupted
[21 -
27].
This obviously depends on the
type of star (and to some extent on the shape of its orbit
around the hole) but for solar-type stars it is
For other types of stars rT scales as
(r* /
R
(ii) The "collision radius" rcoll at which the
velocity dispersion ~ (GMh/r)1/2 is
comparable with the escape velocity from typical stars
[17].
This is significant because the stellar
encounters responsible for the relaxation of the velocity distribution,
energy diffusion, etc., can be treated as elastic Coulomb-type
encounters only outside rcoll: when r
which for other types of stars rcoll scales as
(r* /
R
A "cusp" in the stellar distribution, established by stellar-dynamical
processes, could exist only at radii between rh and
rcoll. Whereas these radii are very different in globular
clusters, for a typical galactic nucleus with vc
Even if the "cusp" is unimportant, tidal disruption of stars
in the core by a massive black hole can provide a supply of
gaseous debris. The energy required to disrupt the star comes
from the orbital kinetic energy. This means that the gaseous
debris will be bound to the hole unless the star enters the hole's
"sphere of influence" r
The energy released directly by a collision between two
solar-type stars in a galactic nucleus or in an r-7/4
stellar cusp
would never be much more than Gm*2 /
r*(~ 10-5 m*
c2).
Really energetic collisions would occur only if compact stars
were involved, or if a distribution of stars had managed to form
(via, for instance, fragmentation of a massive disk) at radii
rcoll.
When Mh grows to exceed 108
M
Note that the concept of the "accretion radius"
GMh/cs2,
where cs is the sound speed, is never very useful in
the context
of gas dynamics in galactic nuclei. Not only is the gas likely to
be inhomogeneous, but the escape velocity from the region
where it is produced, and where the gravitational field of the
point mass Mh is dynamically dominant, generally far exceeds
cs. This conclusion is unlikely to be altered even if the
radiative heating due to the central source itself (Compton heating by
X-rays, photoionization by X-days and UV, and free free and
induced Compton heating by the radio and infrared continuum)
is self-consistently taken into account.
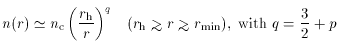
 n(r) r2
tR-1) is independent of r. If the
stars have a range of masses, the cusp
will be populated preferentially by those of higher mass.
n(r) r2
tR-1) is independent of r. If the
stars have a range of masses, the cusp
will be populated preferentially by those of higher mass.
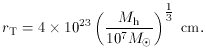
 )(m* /
M
)(m* /
M )-1/3.
There will be an intermediate range of radii around rT
at which
tidal effects would partially disrupt or merely distort the star
rather than destroying it completely. This possibility of "partial
rip-off" is particularly important for giant stars with dense cores
but very extensive atmospheres. These processes may still be
able to reduce the orbital energy by an amount sufficient
to remove stars from the cusp, and capture them into very
tightly-bound orbits passing close to the tidal radius. Such
orbits would rapidly circularise, the liberated energy being
sufficient to disrupt the star.
)-1/3.
There will be an intermediate range of radii around rT
at which
tidal effects would partially disrupt or merely distort the star
rather than destroying it completely. This possibility of "partial
rip-off" is particularly important for giant stars with dense cores
but very extensive atmospheres. These processes may still be
able to reduce the orbital energy by an amount sufficient
to remove stars from the cusp, and capture them into very
tightly-bound orbits passing close to the tidal radius. Such
orbits would rapidly circularise, the liberated energy being
sufficient to disrupt the star.
 rcoll,
two stars cannot deflect each other's velocities through a large angle
without coming so close that they actually collide. For solar type stars,
rcoll,
two stars cannot deflect each other's velocities through a large angle
without coming so close that they actually collide. For solar type stars,
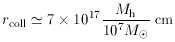
 )
(m* /
M
)
(m* /
M )-1.
A star cannot work its way down into a tightly bound orbit
with r << rcoll without colliding with
another. Such collisions would lead to coalescence at r
)-1.
A star cannot work its way down into a tightly bound orbit
with r << rcoll without colliding with
another. Such collisions would lead to coalescence at r
 rcoll, but
to disruption at
r << rcoll, because the kinetic energy of a
typical impact would
greatly exceed that required to unbind the individual stars.
rcoll, but
to disruption at
r << rcoll, because the kinetic energy of a
typical impact would
greatly exceed that required to unbind the individual stars.
 200 km s-1
they differ
(for solar-type stars) by only an order of magnitude. Some
authors have neglected the cusp entirely; and, though its
presence enhances the tidal capture and stellar collision rate, it
does not alter things by an enormous factor
[21,
23,
29].
200 km s-1
they differ
(for solar-type stars) by only an order of magnitude. Some
authors have neglected the cusp entirely; and, though its
presence enhances the tidal capture and stellar collision rate, it
does not alter things by an enormous factor
[21,
23,
29].
 rh
with a velocity vc, exceeding
(Gm* / R*)1/2. It would
nevertheless be energetically possible
for a small fraction of the debris to fall into the hole and release
enough energy to expel the remainder completely. For this
reason, the rate
rh
with a velocity vc, exceeding
(Gm* / R*)1/2. It would
nevertheless be energetically possible
for a small fraction of the debris to fall into the hole and release
enough energy to expel the remainder completely. For this
reason, the rate  at which a
black hole grows may be below
the rate at which tidal debris is produced. Hills
[21,
27] has
considered the properties of the so-called "debris cloud" and
remarks that the expected velocity dispersion within it is com-
parable with the velocities inferred from the spectra of type II
Seyferts. The material has an initial binding energy corresponding to
that of an orbit with major axis ~ rcoll, but its angular
momentum is very small:
at which a
black hole grows may be below
the rate at which tidal debris is produced. Hills
[21,
27] has
considered the properties of the so-called "debris cloud" and
remarks that the expected velocity dispersion within it is com-
parable with the velocities inferred from the spectra of type II
Seyferts. The material has an initial binding energy corresponding to
that of an orbit with major axis ~ rcoll, but its angular
momentum is very small: 
 2 times that of a circular orbit
at radius rT(<< rcoll). The gas from
tidally disrupted stars thus
moves initially on almost radial orbits. (Debris from a pair of
stars destroyed by a collision at r
2 times that of a circular orbit
at radius rT(<< rcoll). The gas from
tidally disrupted stars thus
moves initially on almost radial orbits. (Debris from a pair of
stars destroyed by a collision at r
 rcoll would
have larger
angular momentum; but unless the orbits of all stars were
similarly oriented, the net specific angular momentum of the
whole cloud would again be low.)
rcoll would
have larger
angular momentum; but unless the orbits of all stars were
similarly oriented, the net specific angular momentum of the
whole cloud would again be low.)
 (or
109 M
(or
109 M for a Kerr
hole), solar.type stars can be swallowed whole, though giants
would still have their envelopes ripped off. Recent work by
Frank [29]
suggests that the mass supply needed for the most
powerful quasars cannot come solely from stellar disruption or
collisions in the cusp.
for a Kerr
hole), solar.type stars can be swallowed whole, though giants
would still have their envelopes ripped off. Recent work by
Frank [29]
suggests that the mass supply needed for the most
powerful quasars cannot come solely from stellar disruption or
collisions in the cusp.