3. MODES OF ACCRETION

If the inflowing material has a large specific angular momentum about a well-defined axis, then one might expect an accretion disc. By adopting the well-known assumptions widely used in applications to X-ray sources (viscosity parametrised by an "a-law", energy radiated thermally, etc.) and simply scaling up M and 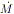, one finds that the radiation emerges predominantly in the soft X-ray and ultraviolet part of the spectrum. For a given M / 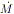, the characteristic temperature at a given value of (r/r_s) scale as M_h^-1/4, so T is ~ 100 times lower for a "critical" disk around a 10⁸ M black hole than it is for the putative disk in a stellar-mass X-ray source like Cygnus X1. 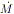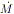A consequence of this lower temperature is that radiation pressure is even more overwhelmingly dominant (by a factor ~ ( / _crit)² (kT/m_pc²)^-1 (r/r_s)^-3/2). This means that the instabilities which probably invalidate the steady disk model for X-ray sources (except in a broad time-averaged sense) would be even more serious here. Models for "thick" disks where radiation pressure is important in the radial as well as the vertical direction, have been discussed by Kozlowski et al [30], and by Lynden-Bell in these proceedings. Models of this kind can persist only if special assumptions are made about the viscosity and dissipation.

In any case, a steady disk emitting thermal radiation gives the wrong spectrum for a quasar. The fraction of energy radiated at optical wavelengths is too low: it could perhaps be raised if either the outer part of the disk were heated by absorbing soft X-rays or ultraviolet radiation from the inner region (though this is a problem because the outer part of the disk is thin and so intercepts only a small fraction of this radiation) or if a strong wind from a "super-critical" inner region flattens the r^-3 dependence of surface brightness in the standard model (and reduces the dominance of the radiation from the hot inner region) or degrades the XUV radiation into the optical band.

An interesting alternative is that the energy dissipated in the inner region goes into relativistic particles and non-thermal radiation: via thermal instabilities [12], via "flaring" of a tangled magnetic field [10, 31], or, if the disk has an ordered field perpendicular to its plane, by an effect analogous to the Goldreich-Julian pulsar model [32]. The energy of the inward- spiralling material would then go into relativistic particles, which would produce a non-thermal continuum away from the plane of the disk. This continuum would be more efficient at irradiating the cool outlying parts of the disk because it would be incident at a large rather than a glancing angle.