


3.2. Dissipative quasi-spherical accretion
When material with low specific angular momentum falls into a black
hole, the resulting radiative output may be negligible (i.e.,
 << 1)
if the inflow is laminar. However, if the inflow is irregular,
dissipative processes (turbulence, shock waves, etc.) could in
principle liberate an amount of energy ~ c2
(r/rs)-1 per unit mass at
radii
<< 1)
if the inflow is laminar. However, if the inflow is irregular,
dissipative processes (turbulence, shock waves, etc.) could in
principle liberate an amount of energy ~ c2
(r/rs)-1 per unit mass at
radii  r. Provided
that the cooling timescale is short enough to
ensure that, at all r, the gas can radiate this energy on the inflow
timescale, the efficiency can be just as high for this mode of inflow
(which I shall term "quasi-spherical dissipative accretion")
[33,
34]
as for the well-known accretion disk.
r. Provided
that the cooling timescale is short enough to
ensure that, at all r, the gas can radiate this energy on the inflow
timescale, the efficiency can be just as high for this mode of inflow
(which I shall term "quasi-spherical dissipative accretion")
[33,
34]
as for the well-known accretion disk.
Defining  (T), the
usual "cooling function", such that the power
emitted per unit volume is (ne2)
(T), the
usual "cooling function", such that the power
emitted per unit volume is (ne2)
 (T), the gas
temperature T(r) at which
cooling balances dissipative heating is given by
(T), the gas
temperature T(r) at which
cooling balances dissipative heating is given by
The infall timescale is tinfall (which may be longer
than tfree fall if pressure
gradients or rotation are important), and during that time each
electron must radiate an energy ~ kTvirial
If cooling is very efficient, most of the gas will stay at ~ 104 K,
the radiation emerging as lines and continuum in the optical or near
ultraviolet (though harder radiation may emerge from elements of gas
just behind shock fronts). But there is an obvious thermodynamic
requirement that T > Tmin, where
Tmin is the temperature of a black body
which radiates L(< r) /
4
When accretion onto a black hole of < 108
M
It is clear from (5) that the cooling will be maximally efficient
when
But in the other extreme, when bremmstrahlung and line cooling are
inefficient, the gas will heat up almost adiabatically (i.e.,
T
The sharp bifurcation between the form of T(r) for the cases of
"efficient" and "inefficient" cooling is a consequence of the form of
the cooling curve: the value of
Note that M does not appear explicitly. Thus, even when
A further quantity of interest in accretion theory is the "trapping
radius" rtrap, within which radiation is transported
inward with the flow
faster than it can diffuse out relative to the matter. This is the
radius such that
Equation (7) shows that, for any dissipative accretion flow when
L
One can then get variability on timescales down to ~
rs / c(~ 1 hr for
Mh
One might conjecture that the so-called "Lacertids" are objects
where cooling is inefficient (Q
Equation (6) yields a lower limit to the size of a region from which
emission lines can originate. (This will be the radius of the
photosphere in the case of quasi-spherical dissipative accretion, but
is a general limit insensitive to any details of the model.) The
characteristic virial velocity or escape velocity, ~
(rmin / rs)-1/2 c, is
thus ~ 104 km s-1. A large value could result only
if the central mass exceeded 108
M
The specific angular momentum of the infalling material, and the
extent to which the resulting spin axis possesses long-term stability,
depends on the origin of the accreted gas. However, it seems in any
case unlikely that the inflow will be smooth or laminar. If Q << 1
(eq. (7)), one would expect the gas whether in a disk or not - to
develop a "two phase" structure: cool clouds at ~ 104 K in pressure
balance with gas at ~ Tvirial (the fraction in the
latter phase adjusting itself so that, for it, Q
There is obviously a tendency for accretion-driven sources to
stabilize at a value comparable with the "Eddington limit"
LEdd
Supercritical accretion can also readily occur when stellar
destruction provides the gas supply. Radiation pressure has a
negligible effect on the bulk motion of a star (though it may, for
instance, cause evaporation from its surface - a further interesting
process that could augment the gas supply). If the stellar density
were high enough, tidal disruption could supply, in effect, an
arbitrarily powerful "shell source" at r
Gas at ~ 104 K can of course be ejected by radiation pressure even
if L < LEdd, because of the opacity due to
lines and the
photoionization continuum. This process is discussed in detail in the
contributions by Goldreich and Kippenhahn. Such effects would be
particularly effective in the high-density photospheric region
envisaged here. When "two phase" accretion occurs, one could have a
flow pattern where the hot material is falling in, but the cool clouds
(on which radiation pressure acts more effectively) are accelerated
outwards. Note however that even electron-scattering opacity can lead
to very high terminal velocities if the acceleration starts at r
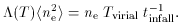
 (GMhmp / r). If the dissipation
results from each element of gas being shock-heated one or more times
during the infall, then the time-averaged value of T
appears on the LHS of eq. (5).
(GMhmp / r). If the dissipation
results from each element of gas being shock-heated one or more times
during the infall, then the time-averaged value of T
appears on the LHS of eq. (5).
 r2 per unit
area. L(< r) is defined as the
luminosity emerging from radii < r; and so
r2 per unit
area. L(< r) is defined as the
luminosity emerging from radii < r; and so
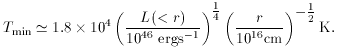
 (i.e.,
rs 3 x 1013
cm) generates a quasar-level luminosity, then, even if cooling is very
efficient, the temperature cannot be as low as ~ 104 K in the
central
regions (r
(i.e.,
rs 3 x 1013
cm) generates a quasar-level luminosity, then, even if cooling is very
efficient, the temperature cannot be as low as ~ 104 K in the
central
regions (r  100rs) where most of the energy is generated. Moreover,
the radiation emerging from these regions may not escape directly,
because a corollary of the assumed efficient cooling is that the
opacity would be high as well. The energy would then all emerge from
an effective photosphere at radius such as Tmin
100rs) where most of the energy is generated. Moreover,
the radiation emerging from these regions may not escape directly,
because a corollary of the assumed efficient cooling is that the
opacity would be high as well. The energy would then all emerge from
an effective photosphere at radius such as Tmin
 104 K.
104 K.
 is high and/or the infall
is "lumpy" (so that < ne2 > >>
< Ne >2
(If, as in disk accretion, the infall timescale is much longer than
the free fall timescale, the cooling is of course efficient enough to
guarantee T(r) << Tvirial for a wider range of
parameters.)
is high and/or the infall
is "lumpy" (so that < ne2 > >>
< Ne >2
(If, as in disk accretion, the infall timescale is much longer than
the free fall timescale, the cooling is of course efficient enough to
guarantee T(r) << Tvirial for a wider range of
parameters.)
 Tvirial) until at r
Tvirial) until at r
 103
rs the electrons get relativistic. At this stage
a variety of more efficient cooling processes - e.g., pair production,
synchrotron, Compton, etc. - can come into play. Some of these cooling
processes depend on the radiation density, magnetic field, etc, and
they do not necessarily depend on the square of ne;
but in general the
effective value of
103
rs the electrons get relativistic. At this stage
a variety of more efficient cooling processes - e.g., pair production,
synchrotron, Compton, etc. - can come into play. Some of these cooling
processes depend on the radiation density, magnetic field, etc, and
they do not necessarily depend on the square of ne;
but in general the
effective value of  (T)
swoops sharply upwards when T
(T)
swoops sharply upwards when T
 1010 K,
guaranteeing that the
overall efficiency of dissipative accretion (i.e., the amount radiated
before gas falls into the hole) is always high, even for low
1010 K,
guaranteeing that the
overall efficiency of dissipative accretion (i.e., the amount radiated
before gas falls into the hole) is always high, even for low
 . We
would then expect the radiation to be emitted from regions near the
hole by non-thermal processes (i.e., in the form of photons with
h
. We
would then expect the radiation to be emitted from regions near the
hole by non-thermal processes (i.e., in the form of photons with
h <<
kT. The absence of cool surrounding gas means that this radiation
could escape without being absorbed.
<<
kT. The absence of cool surrounding gas means that this radiation
could escape without being absorbed.
 (T) is high at
104-105 K, and does
not rise to a higher value until T
(T) is high at
104-105 K, and does
not rise to a higher value until T
 109 K, when
relativistic
processes come into play. If cooling cannot balance the dissipative
heating at 104-105, a rise to relativistic
temperatures is
inevitable. Furthermore it is "touch and go" whether or not efficient
non-relativistic cooling can occur. The relevant parameter is Q =
(tcool(T) / tinfall) x
(Tvirial / T), which must be
109 K, when
relativistic
processes come into play. If cooling cannot balance the dissipative
heating at 104-105, a rise to relativistic
temperatures is
inevitable. Furthermore it is "touch and go" whether or not efficient
non-relativistic cooling can occur. The relevant parameter is Q =
(tcool(T) / tinfall) x
(Tvirial / T), which must be
 1 for some
T
1 for some
T  Tvirial if cooling is efficient. When kT
Tvirial if cooling is efficient. When kT
 mec2, and the dominant cooling is
bremsstrahlung,
mec2, and the dominant cooling is
bremsstrahlung,
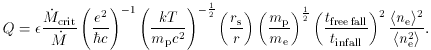


 crit,
efficient cooling demands
crit,
efficient cooling demands  << 1, substantial "clumping" of the gas,
or an inflow velocity slower than free fall. Note also that the
electron-scattering optical depth
<< 1, substantial "clumping" of the gas,
or an inflow velocity slower than free fall. Note also that the
electron-scattering optical depth
 es (> r) is
another quantity which
depends on
es (> r) is
another quantity which
depends on  /
/
 crit. Its value is
crit. Its value is
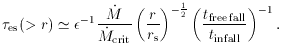
 (> rtrap)
(> rtrap)
 (Vinfall
(rtrap) / c)-1, and its value is given by
(Vinfall
(rtrap) / c)-1, and its value is given by
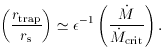
 LEdd and tinfall
LEdd and tinfall
 tfree, the
gas may be only marginally able to radiate
its binding energy on the infall timescale. If cooling is adequate,
then the gas remains at ~ 104 until the black body limit (6)
forces a
higher temperature; and the radiation emerges from a photosphere at ~
104. But if cooling is inadequate at ~ 104,
the gas must heat up until
it becomes relativistic. The radiation will then emerge via
synchrotron-type processes and we shall observe directly non-thermal
radiation emitted near the hole, there being no surrounding gas to
absorb it.
tfree, the
gas may be only marginally able to radiate
its binding energy on the infall timescale. If cooling is adequate,
then the gas remains at ~ 104 until the black body limit (6)
forces a
higher temperature; and the radiation emerges from a photosphere at ~
104. But if cooling is inadequate at ~ 104,
the gas must heat up until
it becomes relativistic. The radiation will then emerge via
synchrotron-type processes and we shall observe directly non-thermal
radiation emitted near the hole, there being no surrounding gas to
absorb it.
 108
M
108
M ), the
continuum being due to the Blandford-Znajek
mechanism, magnetic flares, etc.; and highly polarized if the field is
ordered. Hard X-rays produced by ordinary thermal bremsstrahlung
could also originate from the region r
), the
continuum being due to the Blandford-Znajek
mechanism, magnetic flares, etc.; and highly polarized if the field is
ordered. Hard X-rays produced by ordinary thermal bremsstrahlung
could also originate from the region r
 103
rs.
103
rs.
 1); so that no emission
lines are
seen and any rapidly varying and polarized optical non-thermal
continuum emitted near the hole can escape without reabsorption.
1); so that no emission
lines are
seen and any rapidly varying and polarized optical non-thermal
continuum emitted near the hole can escape without reabsorption.
 . If the width of
the emission lines is indeed
comparable with the orbital or escape velocity from the photospheres,
then we conclude that they are compatible with the model, but that any
significantly broader lines would post problems. Conversely, one could
perhaps adduce the observed line widths as evidence for a high central
mass so compact that it could not be anything other than a black hole.
This conclusion would be strengthened if one could decisively exclude
the (currently conceivable) possibility that the high gas velocities
represent outflow with speeds much exceeding the escape velocity. The
"photospheric" region from which broad emission lines may originate
could be comparable to the photosphere of a hot star in terms of
surface brightness, but it would be much less smooth and
quiescent. One would expect large-amplitude inhomogeneities, and
macroscopic motions up to ~ 104 km s-1 (i.e.,
highly supersonic).
. If the width of
the emission lines is indeed
comparable with the orbital or escape velocity from the photospheres,
then we conclude that they are compatible with the model, but that any
significantly broader lines would post problems. Conversely, one could
perhaps adduce the observed line widths as evidence for a high central
mass so compact that it could not be anything other than a black hole.
This conclusion would be strengthened if one could decisively exclude
the (currently conceivable) possibility that the high gas velocities
represent outflow with speeds much exceeding the escape velocity. The
"photospheric" region from which broad emission lines may originate
could be comparable to the photosphere of a hot star in terms of
surface brightness, but it would be much less smooth and
quiescent. One would expect large-amplitude inhomogeneities, and
macroscopic motions up to ~ 104 km s-1 (i.e.,
highly supersonic).
 1). This possibility would
seem to merit further investigation.
1). This possibility would
seem to merit further investigation.
 1.3
x 1046 (Mh / 108
M
1.3
x 1046 (Mh / 108
M ) erg
s-1. Indeed, this consideration led Zeldovich
and Novikov [8]
to propose as early as 1964 that quasars were powered
by accretion onto black holes of ~ 108
M
) erg
s-1. Indeed, this consideration led Zeldovich
and Novikov [8]
to propose as early as 1964 that quasars were powered
by accretion onto black holes of ~ 108
M . In principle
LEdd can be
exceeded in a variety of ways in any non-spherical models. The inflow
may resemble a very convective "settling solution" with "buoyant
bubbles": a jet with high (P/
. In principle
LEdd can be
exceeded in a variety of ways in any non-spherical models. The inflow
may resemble a very convective "settling solution" with "buoyant
bubbles": a jet with high (P/
 ) may escape along
the rotation axis,
driven by buoyancy (i.e., higher P/
) may escape along
the rotation axis,
driven by buoyancy (i.e., higher P/
 ); or one could have
"two phase"
quasi-spherical accretion with one phase blowing out and the other
falling in (provided, of course, that the net flux of matter is
inward). If
); or one could have
"two phase"
quasi-spherical accretion with one phase blowing out and the other
falling in (provided, of course, that the net flux of matter is
inward). If  >>
>>
 crit, then energy
liberated near the hole (r < rtrap,
eq. (9)) cannot escape unless it is trapped in gas which is moving
bodily outward.
crit, then energy
liberated near the hole (r < rtrap,
eq. (9)) cannot escape unless it is trapped in gas which is moving
bodily outward.
 rT. If this
exceeded LEdd
then some of the material would be blown off as a wind by the pressure
of a supercritical radiation flux, the gravitational energy released
by inflow of the remainder providing the power. The photon luminosity
can exceed LEdd when there is a radiation-driven wind;
and the kinetic
energy of the wind can be converted into radiation when deceleration
occurs at larger distances from the hole, thereby yielding additional
luminosity.
rT. If this
exceeded LEdd
then some of the material would be blown off as a wind by the pressure
of a supercritical radiation flux, the gravitational energy released
by inflow of the remainder providing the power. The photon luminosity
can exceed LEdd when there is a radiation-driven wind;
and the kinetic
energy of the wind can be converted into radiation when deceleration
occurs at larger distances from the hole, thereby yielding additional
luminosity.
 rs
(where, for a settling solution, the effective sound speed is itself ~
c).
rs
(where, for a settling solution, the effective sound speed is itself ~
c).