4. FORMATION AND EVOLUTION OF CLUSTERS

Clusters can be observed at sufficiently large redshifts that evolutionary effects are expected. Indeed, an exciting recent result is the discovery that the X-ray emission from clusters is increasing with cosmic time, even in a sample restricted to redshifts less than about 0.5. This discovery is qualitatively consistent with the expectations of hierarchical models, according to which big clusters would have formed only recently as the outcome of mergers of smaller ones. And it has stimulated further discussion of cluster formation, particularly in the context of specific models.

The most popular and best-defined cosmogonic model is the standard Cold Dark Matter scheme. On the assumption that the fluctuations have the same r.m.s. amplitude on all scales when that scale enters the horizon (the 'Harrison-Zeldovich' spectrum), one can then calculate the r.m.s. fluctuations at the recombination epoch as a function of mass scale M. See Figure 3 and its caption for more explanation. On the further assumption that the amplitude distribution is gaussian, one can set up initial conditions for an N-body simulation which can compute the distribution of the dark matter as a function of cosmic epoch. Work of this kind leads to good quantitative agreement with the properties of individual galactic halos and small groups. Moreover, rich clusters can be interpreted as the outcome of exceptionally high amplitude peaks in the initial noise distribution on mass scales of order 10¹⁵ M.

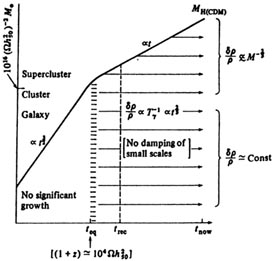
Figure 3. The growth of adiabatic fluctuations in a universe dominated by 'cold dark matter'. The mass of cold dark matter within the particle horizon is shown as a function of time on a log-log plot. For t > teq (corresponding to the redshift indicated on the figure), all scales grow at the same rate. Before teq, when the expansion is radiation-dominated, there is essentially no growth, because the growth timescale much exceeds the expansion timescale. If the fluctuations on all scales enter the horizon with equal amplitude (the 'Harrison-Zeldovich' hypothesis), then the present-day spectrum would have the approximate form written on the right-hand side. The cold dark matter perturbations start to grow at teq, whereas radiation pressure inhibits growth of baryonic fluctuations on relevant scales until the (later) recombination time trec. Cold dark matter fluctuations thus have a 'head start' (baryons being able to fall into the resultant potential well after trec); this permits an acceptable cosmogonic scheme with lower fluctuation amplitude , and smaller microwave background fluctuations, than in a baryon-dominated universe (cf. Fig 5).

It is of course the baryons, particularly the hot gas and the galaxies themselves, which are directly observed, so what is really needed is a simulation which takes account of how the gas evolves, and how it condenses into galaxies. This is a much more challenging computational task, where, as we will hear at this meeting, the first steps are now being taken. However, even without detailed calculations, the CDM model can give a convincing answer to a question which arises in any hierarchical model: namely, what determines the demarcation between an individual galaxy and a cluster? Why is something like the Coma cluster not just a single big galaxy?

The answer to this question depends crucially on the cooling time for gas trapped in a potential well. If this is short compared to the dynamical time, no quasi-static equilibrium is possible, and the gas will fragment into stars, perhaps alter collapsing to a disc. If the cooling is slower than free fall, but still can occur within the Hubble time, then the gas, though quasi-static, will gradually deflate towards the centre of the potential well. If the cooling is slower still, the shock-heated gas in effect remains at the virial temperature. These three regimes are depicted in Figure 4, in a plot of mass versus radius. From this figure, we can see why there is an upper limit to the mass of galaxies. In a hierarchical build up of structure, as in the CDM model, the bound systems at early epochs are dense, and the potential wells are shallow enough that the gas does not get heated to a very high temperature. In these situations, cooling is rapid and effective. But beyond a certain stage, when the potential wells are deeper and the density lower, cooling is less effective. The critical mass, of order 10¹² M, therefore sets an upper limit to the size of a galaxy. If larger aggregates build up by gravitational clustering, the gas within them will remain hot. This is essentially the distinction between a large galaxy and a system such as Coma.

Figure 4. This diagram delineates the mass-radius relation for a self-gravitating gas cloud whose cooling and dynamical timescales are equal (assuming cooling due only to bremsstrahlung, H and He recombination, and line emission). A cloud of given mass whose radius was initially very large would deflate quasistatically (because tcool > tdyn) until it crossed the critical line re; it would then collapse in free fall and could fragment into stars. This simple argument (which can readily be modified to allow for non-spherical geometry, a non-baryonic component of mass, etc.) suggests why, irrespective of the cosmological details, no galaxies form with baryonic masses > 1012 M and radii > 105 pc. There is an intermediate regime, important for clusters and cooling flows, where rc < r < rh, and the clouds are quasistatic but can deflate in less than the Hubble time.