


On the larger scales of superclusters, we cannot assume that the systems
are virialised,
but the gravitational effect of the excess density will cause velocity
perturbations
which are in principle measurable. For a spherical perturbation where the
overdensity is not large enough to cause turnaround, the velocity
perturbation is related to the overdensity, and to
 , by the following equation.
, by the following equation.
where f(
We can readily infer, since gravity and light both obey inverse square
laws, that
the contributions to our peculiar velocity made by any particular galaxy
or group
is proportional to the light which we receive from it, provided that
b is indeed
a constant. We note also that the gravitational potential fluctuation
(
The above equation can be applied to our own local motion just from
two-dimensional data, without knowledge of the redshifts of
galaxies. The next step,
however, is a much more ambitious one, namely to apply the equation to
infer the
mass distribution throughout our local region of space, given adequate
knowledge
of the peculiar velocities of all the galaxies. The peculiar velocities
can, of course,
only be determined if one has a distance indicator which is sufficiently
precise
to distinguish between the actual distance of a galaxy and the distance
it would
have if it was obeying the Hubble flow. The main practical uncertainties in the
measurement and interpretation of largescale streaming stem from the
problems of calibrating the distance indicators.
In principle, however, knowledge of the largescale velocity field would
allow us to infer the mass distribution without any assumption that galaxies
trace mass, or
that the quantity b is a universal ratio. We need only assume
that galaxies are test
particles whose motions are gravitationally induced. The main problems
are still
with the distance measurements, and a lingering uncertainty about whether the
luminosity calibrators (velocity dispersion, diameter, etc.) are really
independent of location and environment.
The expected deviations from Hubble flow are only a few hundred kilometers
per second at most. There is very little hope of ever measuring these
reliably by
existing methods at distances beyond ~ 100 megaparsecs, because they are then
only a very small fraction of the recession velocity, and therefore
would require still
more accurate distance indicators. There are, however, in principle
other quite different
methods which could determine peculiar velocities of clusters at still greater
distances. For instance, there is an extra contribution to the
Sunyaev-Zeldovich
effect due to the bulk motion of the cluster, This is equivalent to a
simple 'moving
mirror' effect, with amplitude equal to the Doppler shift multiplied by
the Compton
optical depth. (Transverse motions, incidentally, would yield
polarization, but this
is a higher order effect and still more challenging for observers.)
What we would really like would be a method of directly delineating the dark
matter distribution on large scales. One possibility which has recently
been suggested
is gravitational distortion of faint background galaxies. A supercluster would
not have such a high column density as the core of a rich cluster, and
therefore could
not give strongly distorted or highly magnified images resembling the
'arcs'. But
even if the induced distribution were small the fact that the angular
diameter of
a supercluster may be of order 1° means that up to 105
galaxies would share a
correlated distortion; so it is by no means hopeless to look for an
effect of only a few per cent.
At the moment one cannot conclusively decide between two extreme views
regarding
the dark matter distribution. On the one hand, it could be that on large
scales the overall mass distribution is smooth, and the apparent
largescale structure
in the galaxy distribution represents simply some largescale spatial
modulation of
the efficiency of galaxy formation. On the other hand, the density of
galaxies could
be a reliable tracer of the dark matter distribution on all scales,
except for a simple biasing factor b.
We can nevertheless say with great confidence that on scales much larger
than 50
megaparsecs the overall mass distribution must be relatively smooth, in
the sense
that the amplitude of the r.m.s. density fluctuations is << 1. Our best
evidence
here comes from the microwave background anisotropies. For scales exceeding the
horizon scale at the epoch of recombination, the dominant contribution
to
Even a mass concentration as large as the Great Attractor would, if
placed on the
last scattering surface, yield a fluctuation little more than 10-5.
The microwave background anisotropies also, as (2) implies, constrain
the potential
fluctuation on mass much larger than 100 megaparsecs, This is of interest
because it allows us to test whether the initial fluctuation spectrum
does indeed
have a power law form. The assumption of a power law is generally made because
it seems unnatural to feed the mass scale appropriate to clusters or
galaxies into
the conditions of the early universe.
Figure 5 summarizes the various
constraints on
the fluctuation amplitude on scales stretching all the way from
sub-stellar masses
up to the Hubble radius and beyond. We see that if the initial
fluctuation spectrum
is a power law, its slope is well constrained. Moreover, if it is a
power law with the
scale-independent Harrison-Zeldovich form, the amplitude is well
constrained to be
a bit less than 10-5. It is perhaps worth noting, however,
that the case for
favoring a Harrison-Zeldovich spectrum would be very much weaker if the
universe were
not, as theorists like to believe, flat with exactly the critical
density. If
It is interesting to ask whether a nearby cluster or supercluster would perturb
the microwave background. The Sachs-Wolfe effect due to the precursor of
a cluster
on the last scattering surface causes a temperature perturbation of
order
But a similar cluster with redshift z < 1 produces a much smaller
effect on the
microwave background. The effect of the cluster's potential well on the
microwave
photons is, to first order, zero: the photons gain energy falling in but
lose it again
climbing out the other side. The only non-zero effects are of higher
order: they are
due to the extra time delay experienced by photons going through the
potential well
of the cluster, and the deepening of the potential well as the photons
go through. For
a linear perturbation of radius r, these effects, the first a
blueshift and the second
a redshift, are both smaller than the Sachs-Wolfe effect by r /
ctH. For a nonlinear
collapsing perturbation the second effect may exceed the first by the
ratio of the
collapse rate to the Hubble expansion rate, but it is still generally
much smaller
than the Sachs-Wolfe effect that would be associated with a similar
cluster observed
in its embryonic state on the surface of last scattering.
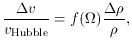
 )
)
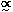
 0.6. The
overdensity factor
0.6. The
overdensity factor 
 /
/
 may
not be equal to the overdensity
in luminous galaxies. Indeed it is customary to regard these quantities
as related
by a bias factor b. Our local peculiar velocity, measurable by
our motion through the microwave background, is generally thought to
have been induced by inhomogeneities
in the distribution of galaxies around us. Clusters pull, and voids in effect
'push', our Local Group.
may
not be equal to the overdensity
in luminous galaxies. Indeed it is customary to regard these quantities
as related
by a bias factor b. Our local peculiar velocity, measurable by
our motion through the microwave background, is generally thought to
have been induced by inhomogeneities
in the distribution of galaxies around us. Clusters pull, and voids in effect
'push', our Local Group.

 M/R)
required to cause a given dv
(
M/R)
required to cause a given dv
(
 M/R2) is
larger if the scale is larger.
M/R2) is
larger if the scale is larger.
 T/T
comes from the gravitational potential or metric fluctuations on the
last scattering
surface. This is the so-called 'Sachs-Wolfe' effect. The upper limits
are of order
10-5, and these imply that on the corresponding scale
L(~
T/T
comes from the gravitational potential or metric fluctuations on the
last scattering
surface. This is the so-called 'Sachs-Wolfe' effect. The upper limits
are of order
10-5, and these imply that on the corresponding scale
L(~
 ctH) we must have
ctH) we must have
 differs
significantly from unity, there is a preferred length scale in
the universe, essentially
the Robertson-Walker curvature radius. Given that this scale, a
substantial fraction
of the present Hubble radius, would have to have been imprinted at an
early time,
it would then be by no means implausible to suppose that other scales,
related to
it by some modest numerical factor, might also have been singled out.
differs
significantly from unity, there is a preferred length scale in
the universe, essentially
the Robertson-Walker curvature radius. Given that this scale, a
substantial fraction
of the present Hubble radius, would have to have been imprinted at an
early time,
it would then be by no means implausible to suppose that other scales,
related to
it by some modest numerical factor, might also have been singled out.

 / c2,
where
/ c2,
where  is the Newtonian potential;
this is of order v2 / c2 where v
is the velocity
dispersion in the cluster after virialisation.
is the Newtonian potential;
this is of order v2 / c2 where v
is the velocity
dispersion in the cluster after virialisation.