The notation used to describe observational relations in cosmological models varies greatly in the literature. Therefore, in order to maintain some consistency at least among the papers which deal directly with relativistic cosmology, here I shall attempt to follow as much as possible the definitions and notation similar to the ones used by Ellis (1971, p. 144).
Let us call F the bolometric flux as measured by the observer. This is the rate at which radiation crosses unit area per unit time in all frequencies. Then FG will be the bolometric galaxy flux measured across an unit sphere located in a locally Euclidean space at rest with the galaxy (2)
The distance definitions used here are three: i) the observer
area distance r0 is the area distance of a source
as measured by the
observer (3) ;
ii) the galaxy area distance
rG is defined as the area distance to the
observer as measured from the distant galactic source. This quantity is
unobservable, by definition; iii) the luminosity distance
d
is the distance
measured by the observer as if the space were
flat and nonexpanding, that is, as if the space were stationary and
Euclidean. These three definitions of distance are related to each other
by Etherington's reciprocity theorem
(Ellis 1971,
p. 153;
Schneider et al. 1992,
p. 111, 116),
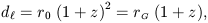
| (1) |
where z is the redshift of the source. Notice that all these distances tend to the same Euclidean value as z -> 0, but greatly differ at large z.
Let us now call L the bolometric source luminosity, that is, the
total rate of radiating energy emitted by the source and measured
through an unity sphere located in a locally Euclidean spacetime
near the source. Then 
will be the
observed frequency
of the radiation, and
G the emitted
frequency, that is, the frequency of the same radiation
received by the observer, but at rest-frame of the emitting galaxy.
The source spectrum function
J(G)
gives the proportion of radiation emitted by the source at a certain
frequency G as measured at
the rest frame
of the source. This quantity is a property of the source, and since
it gives the percentage of emitted radiation, it obeys the following
normalization condition,
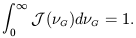
| (2) |
Considering this definition, then
LG =
L J(G) is
the specific
source luminosity, and gives the rate at which radiation is
emitted by the source at the frequency
G
at its locally Euclidean rest frame. Then, to summarize, the following
expressions give the relationship between flux and luminosity:
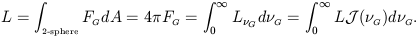
| (3) |
The redshift z is, by definition, given by,
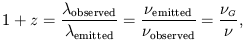
| (4) |
and from this expression it follows that
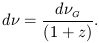
| (5) |
The observed flux, redshift and observer area distance are then related by the equation below (Ellis 1971, p. 156),
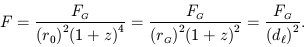
| (6) |
In the context of astronomical measurements, the observed flux is called observed luminosity of the source, and the bolometric apparent magnitude of the source is defined by
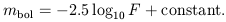
| (7) |
The distance modulus is defined by
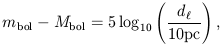
| (8) |
where Mbol is the bolometric absolute magnitude.
The underlying spacetime geometry appears in the expressions for the redshift and the different definitions of distance. That can be seen if we remember that in the general geometric case the redshift is given by (Ellis 1971, p. 146),
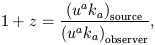
| (9) |
where ua is the observer's four-velocity, and ka is the tangent vector of the null geodesic connecting source and observer, that is, the past light cone. This expression allows us to calculate z for any given spacetime geometry.
Similarly, the observer area distance r0 is, by definition, given by
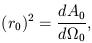
| (10) |
where dA0 is the cross-sectional area of a bundle of
null geodesics
diverging from the observer at some point, and
0 is the
solid angle subtended by this bundle
(Ellis 1971,
p. 153;
Schneider et al. 1992,
p. 110). This quantity can in principle be measured,
but it can also be obtained from the assumed spacetime geometry,
especially in spherically symmetric metrics, from where it can be
easily calculated. For instance, in the Einstein-de Sitter metric,
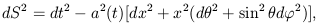
| (11) |
the observer area distance is straightforwardly obtained as being given by
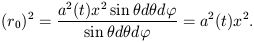
| (12) |
2 Throughout this paper I will generically call any cosmological source by the term ``galaxy''. Back.
3 This definition of distance has different names in the literature. It is the same as Weinberg's (1972) angular diameter distance, and Kristian & Sach's (1966) corrected luminosity distance. Back.