The flux within some specific wavelength range can be calculated if we consider equations (3), (5) and (6). Then we have (see Ellis 1971),
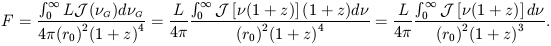
| (13) |
Therefore, the flux measured in the frequency range
, +
d by the observer may be written as
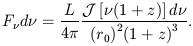
| (14) |
F is also called
specific flux of the radiation.
The apparent magnitude in a specific observed frequency bandwidth is obtained from a different form than given by equation (7), which may written as
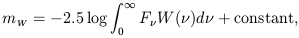
| (15) |
where W() is the function
which defines the spectral interval
of the observed flux (the standard UBV system, for instance). This is
a sensitivity function of the atmosphere, telescope and detecting device.
From equations (14) and (15) the apparent magnitude in a specified spectral interval W may be written as
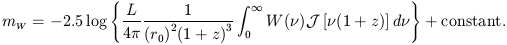
| (16) |
Some remarks about this equation are important to mention. Firstly,
equation (16) calculates the apparent magnitude of a source
whose intrinsic luminosity at a specific redshift is somehow
known. Secondly, in a similar manner this equation can also be used to
calculate the intrinsic luminosity of a cosmological source whose redshift
and apparent magnitude are known from observations. Finally, since
cosmological sources do evolve, the intrinsic luminosity L
changes according to the evolutionary stage of the source, and
therefore, L is actually a function of the redshift; L =
L(z). Hence,
in order to use equation (16) to obtain the apparent
magnitude evolution of the source, some theory for luminosity evolution
is also necessary. For galaxies, L(z) is usually derived
taking into
consideration the theory of stellar evolution, from where some simple
equations for luminosity evolution can be drawn (see
Binney &
Tremaine 1987,
p. 552;
Peebles 1993,
p. 330, and references therein).
(4)
Finally, since J[(1 +
z)] is
a property of the source at a specific redshift, this function must
be known in order to calculate the apparent magnitude, unless the
K-correction approach is used (see below).
For magnitude limited catalogues, the luminosity distance and the observer area distance have both an upper cutoff, which is a function of the apparent magnitude, the frequency bandwidth used in the observations and the luminosity of the sources. Considering equation (1), the luminosity distance of flux limited sources may be written as
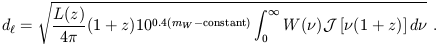
| (17) |
The relations above demand the knowledge of both the source spectrum and the redshift. However, when the source spectrum is not known, it is necessary to introduce a correction term in order to obtain the bolometric flux from observations. This correction is known as the K-correction, and it is a different way for allowing the effect of the source spectrum.
The method that will be presented next for deriving the K-correction
follows the classical work of Humason, Mayall and Sandage
(1956,
appendix B; see also
Oke & Sandage
1968,
Sandage 1988,
1995).
We start by
calculating the difference in magnitude produced by the bolometric
flux F and the flux
FW measured by the observer, but at the bandwidth
W() in any redshift
z. Therefore,
I shall write both quantities as F(z) and
FW(z)
respectively. Since, by definition, we know that
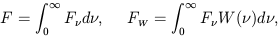
| (18) |
the difference in magnitude
m(z) will be given by
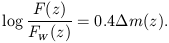
| (19) |
The rate between the observed flux FW(z) at a given redshift and at z = 0 defines the K-correction. Then, considering equation (19), we have that
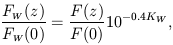
| (20) |
where we have defined
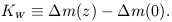
| (21) |
Then it follows that
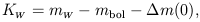
| (22) |
which means that once we know the K-term and the observed magnitude
mW, the bolometric magnitude is know within a
constant m(0). If we
now substitute equation (14)
into equation (20), it is easy to show that
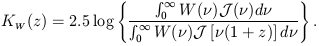
| (23) |
Remembering that by equation (5) we know that we can have
the source spectrum transformed from the rest frame of the source
to the rest-frame of the observer by a factor of (1 + z), that is,
J[(1 + z)]
d =
[J(G)
dG] /
(1 + z), then we may also write equation (23) as
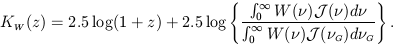
| (24) |
Note that the equations above allow us to write theoretical K-correction expressions for any given spacetime geometry, provided that the line element dS2 is known beforehand. These theoretical expressions for observables like the K-correction could, in principle, be directly compared with observations.
As a final remark, it is obvious that if the source spectrum is already known, all relevant observational relations can be calculated without the need of the K-correction.
With the calculations above we can obtain the theoretical expression for the colour of the sources for any given spacetime. Let us consider two bandwidths W and W'. From equation (16) we can find the difference in apparent magnitude for these two frequency bands in order to obtain an equation for the colour of the source in a specific redshift. Let us call this quantity CWW'. Thus,
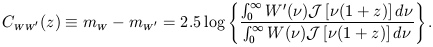
| (25) |
Considering that cosmological sources do evolve, they should emit different luminosities in different redshifts due to the different evolutionary stages of the stellar contents of the sources, and this is reflected in the equation above by the source spectrum function which may be different for different redshifts. Note, however, that in the equation above the source is assumed to have the same bolometric luminosity in a specific redshift and, therefore, we can only use equation (25) to compare observation of objects of the same class and at similar evolutionary stages in certain z, since L = L(z). This often means galaxies of the same morphological type. In other words, equation (25) is assuming that a homogenous populations of cosmological sources do exist, and hence, the evolution and structure of the members of such a group will be similar.
Equation (25) also gives us a method for assessing the
possible evolution of the source spectrum. For instance, by calculating
B - V and V - R colours for E galaxies with modern determinations of
the K-correction, Sandage
(1995,
p. 50) reported that no colour
evolution was found to at least z = 0.4. However, for z
0.3
it was found that rich clusters of galaxies tend to be bluer (the
Butcher-Oemler effect) than at lower redshifts
(Peebles 1993,
p. 202; see also
Kron 1995,
p. 299). Therefore, if we start from a certain
metric, we can calculate the theoretical redshift range where colour
evolution would be most important for the assumed geometry of the
cosmological model.
Another point worth mentioning, from equation (25) we see that colour is directly related to the intrinsic characteristics of the source, its evolutionary stage, as given by the redshift and the assumptions concerning the real form of the source spectrum function at a certain z. However, this reasoning is valid for point sources whose colours are integrated and, therefore, we are not considering here structures, like galactic disks and halos, which in principle may emit differently and then will produce different colours. If we remember that cosmological sources are usually far enough to make the identification and observation of source structures an observational problem for large scale galaxy surveys, this hypothesis seems reasonable at least as a first approximation.
As a final remark, it is clear that in order to obtain a relationship between apparent magnitude and redshift we need some knowledge about the dependence of the intrinsic bolometric luminosity L and the source spectrum function J with the redshift. It seems that such a knowledge must come from astrophysically independent theories about the intrinsic behaviour and evolution of the sources, and not from the underlying spacetime geometry.
In any cosmological model if we consider a small affine parameter
displacement dy at some point P on a bundle of past null geodesics
subintending a solid angle
d
0, and if
n is the number density
of radiating sources per unit proper volume at P, then the number
of sources in this section of the bundle is
(Ellis 1971,
p. 159)
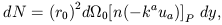
| (26) |
where, as before, ka is the propagation vector of the
radiation
flux and ua is the 4-velocity of the observer. Equation
(26) considers the counting of all sources at P
with number density n. Consequently, if we want to consider the
more realistic situation that only a fraction of galaxies in the
proper volume dV = (r0)2
d0
dl = (r0)2
d0
(- kaua)dy is actually
detected and included in the
observed number count, we have to write dN in terms of a
selection function 
which
represents this detected fraction of galaxies. Then equation (26) becomes
(Ellis et al. 1985)
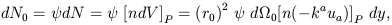
| (27) |
where dN0 is the fraction number of sources actually observed in the unit proper volume dV with a total of dN sources.
In principle can be estimated from
a knowledge of the
galactic spectrum, the observer area distance, the redshift, and
the detection limit of the sample as given by the limiting flux in
a certain frequency bandwidth. The other quantities in equation
(27) come from the assumed cosmological model itself,
and inasmuch as equation (27) is general, it is valid
for any cosmological model, either homogeneous or inhomogeneous.
In order to determine we need to
remember that in any
spacetime geometry the observed flux in bandwidth W is given by
equations (14) and (18),
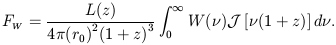
| (28) |
Then, if a galaxy at a distance r0 is to be seen at flux
FW, its luminosity L(z) must be bigger
than {4
(r0)2
(1+z)3 FW} /
{
0
W()
J[(1 + z)]
d}. Therefore, the probability
that a galaxy at a distance r0
and with redshift z is included in a catalog with maximum
flux FW is,
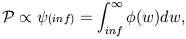
| (29) |
where this integral's lower limit is
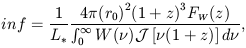
| (30) |
L* is a parameter, and
(w) is the luminosity
function. model L* is a characteristic
luminosity at which the
luminosity function exhibits a rapid change in its slope.
Now, if we assume spherical symmetry, then equation (27) becomes
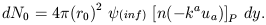
| (31) |
Thus, the number of galaxies observed up to an affine parameter y at a point P down the light cone, may be written as
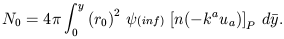
| (32) |
All quantities in the integrand above are function of the past null cone affine parameter y, and, in principle, they must be explicitly calculated before they can be entered into equation (32). In some cases one may avoid this explicit determination and use instead the radial coordinate, a method which turns out to be easier than finding these expressions in terms of y (Ribeiro 1992). Then, once N0(y) is obtained, it becomes possible to relate it to other observables, since they are all function of the past null cone affine parameter. For example, if one can derive an analytic expression for the redshift in a given spacetime, say z = z(y), and if this expression can be analitically inverted, then we can write N0 as a function of z.
It is important to mention that the local number density n is given in units of proper density and, therefore, in order to take a proper account of the curved spacetime geometry, one must relate n to the local density as given by the right hand side of Einstein's field equations. If, for simplicity, we suppose that all sources are galaxies with a similar rest-mass MG, then
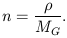
| (33) |
An indication on how to use the expressions above can be grasped
for the Einstein-de Sitter model, where it is well-known that the
local density 
may be
written as
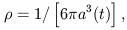
| (34) |
where
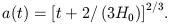
| (35) |
If we remember that from a relativistic viewpoint astronomical observations are actually made along the past light cone, where dS2 = 0, we must calculate a(t) and find its expression along the backward null cone,
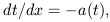
| (36) |
before we can use equation (33) back into equation (32).
From the discussion above it is clear that the theoretical
determination of N0 depends critically on the
spacetime geometry
and the luminosity function . For
the latter, in the
Schechter (1976)
model it has the form
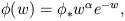
| (37) |
where * and
are constant parameters. One
must not forget that this luminosity function shape was originally
determined from local measurements
(Schechter 1976),
and there is now a controversy about the change of shape and parameters
of the luminosity function in terms of evolution
(Lonsdale &
Chokshi 1993;
Gronwall & Koo
1995;
Ellis et al. 1996),
that is, as we go
down the light cone. In any case the Schechter's function above can
be used at least as a starting point. In addition, since the
luminosity function is being used as a probability in equation
(29), it must be properly normalized. However, considering
equation (32) one can choose the number density n to
agree with the normalization of .
As a final remark, one must note that gravitational lensing magnification can also affect the counting of point sources, because weak sources with low flux might appear brighter due to lensing magnification. Such an effect will not be treated here, since its full treatment demands more detailed information about the sources themselves, such as considering them as extended ones, and is considered to be most important for QSO's (see Schneider et al. 1992).
4 Note that equation (16) also indicates that the source spectrum function J might evolve and change its functional form at different evolutionary stages of the source. Back.