Luminosity Distributions

Reviews:

1. Holmberg, E. in Galaxies and the Universe (Sandage, A., Sandage, M., & Kristian, J., eds.) = Stars and stellar Systems Vol. IX, Univ. Chicago Press (1975). p. 123.
2. The World of Galaxies (H.C. Corwin Jr., & L. Bottinelli, eds.), Berlin, Springer (1989).
3. The Magellanic Clouds (R. Haynes, & D. Milne, eds.), Int. Astron. Union Symp. 148, Dordrecht, Kluwer (1991).

Surface Photometry of Elliptical Systems

The radial surface-brightness distribution of the brighter elliptical galaxies (M_V < -15 mag) and compact dwarf systems follows closely the empirical law.

1. de Vaucouleurs, G. in Stellar Systems (Figure, S., ed.), Hdb. Physik 59, Springer, Berlin (1959). p. 311.
2. de Vaucouleurs, G. Mon. Not. R. Astron. Soc. 113 (1953) 134.
3. Kormendy, J., & Djorgovski, S., Annu. Rev. Astron. Astrophys. 27 (1989) 235.

1. Nguyen, Q., Jackson, J.M., Henkel, C., Truony, B., & Mauersberger, R., Astrophys. J. 399 (1992) 521.
2. Gallimore, J.F., Baum, S.A., O'Dea, C.P., Brinks, E., & Pedlar, A., Astrophys. J. 422 (1994) 13.

log I() = -3.33 (1/4 - 1)

(1)

with = R / R_e

R_e = effective radius = radius (or major axis) of that isophote inside which half of the total light is emitted

I() = surface brightness at distance from the center along the major axis.

The formula fails only in the innermost and in the outermost parts. Another representation is given by King's model [King, I.R. Astron. J. 71 (1966) 64].

The distribution is similar to an isothermal sphere. The similarity of I() for all normal ellipticals means that they are all now in a fairly similar dynamical state.

For variation of the ellipticity of the isophotes within individual galaxies.

The specific intensity I_e at R_e or the corresponding surface brightness µ_e in [mag per unit solid angle] is related to the average surface brightness µ'_e within R_e; for an ^1/4 distribution

In the denser systems the ^1/4 law apparently applies right up to the center. Here, according to Eq. (1), the surface brightness should be 2.5 × 3.33 = 8.3 mag brighter than at R_e, thus

The range of µ'_e in dense systems is from 19.5 to 21.5 mag(B)/arcsec² (corresponding to about 1200...200 L pc^-2).

Supergiant elliptical systems show an elliptical-like core in an extended outer envelope.

Carter, D. [Mon. Not. R. Astron. Soc. 178 (1977) 137] investigated the optical extent of four giant elliptical and cD galaxies, and in two of them he found no indication of the convergence of the total luminosity of the galaxy.

Low-density dwarf spheroidal systems (M_V > -15) do not obey the ^1/4 law. The light concentration is slight and the central core with radius R R_e/2 has a nearly constant surface brightness. But the surface brightness drops off more rapidly in the outer parts than for giant systems. The Fornax system (dE) has µ'_e = 24.8 mag/arcsec² ( 9 L pc^-2) or about 1% of the corresponding luminosity density in the compact dwarf E 2 system M 32. Preliminary photometries of Sculptor and other nearby dwarfs indicate even lower densities. Large numbers of dwarfs with such densities might remain undetectable by current techniques.

Galaxy Luminosity Classification: [Ohta, K., Sasaki, M., Yamada, T., Saito, M., & Nakai, N., Pub. Astron. Soc. Japan. 44 (1992) 585].

Spiral Systems:

Edge-on spirals and S0 galaxies clearly show two main structural components, a flat disk and a spherical bulge. The bulge varies in its relative importance from dominant to zero (see Fig. 3). Luminosity distribution of the bulge (characteristic for ellipticals, see above):

log I1 () 1/4,

(4)

luminosity distribution of the flat component (characteristic for disks of late spirals)

I2(R) = I0 e-R   or   log I2(R) = const - R

(5)

i.e. an exponential luminosity law. is the inverse of the scale length ; it is measured by the photometric gradient

G(R) = d(log I) / dR,   thus   = 0.4343 / G(R) .

(6)

For a purely exponential law: effective radius R_e = 1.6785 . The relations corresponding to Eq. (3) are:

From an investigation of 36 exponential disks Freeman, K.C. [Astrophys. J. 160 (1970) 811] arrived at the following conclusions:

a) has a range of one order of magnitude from 0.5 to 5 kpc for types earlier than Sc.

b) For types later than Sc the maximum value of decreases from 5 kpc at Sc (morphological parameter t = 5) to 1 kpc at Im (t = 10), confirming earlier results on the dependence of galaxy diameters on Hubble type.

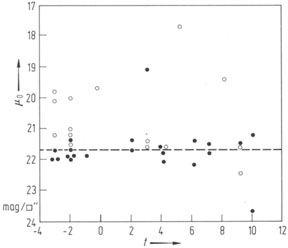
c) For 28 out of 36 spirals and S0 galaxies the exponential disks have nearly the same intensity scale: < µ₀ > = 21.65 mag/arcsec² with a very small standard deviation of 0^m.3, in spite of a large range of 5^M in absolute magnitudes and independent of morphological type from L^-(t = -3) to Im (t = 10), Fig. 2. However, see critical comments in [Burstein, D. in Photometry, Kinematics and Dynamics of Galaxies (Evans, D.S., ed.), University of Texas (1979). p. 81].

Figure 2. Corrected face-on central surface brightness µ0 for exponential disks versus the morphological type t (see [Freeman, K.C. in Galaxies and the Universe (Sandage, A., Sandage, M.; Kristian, J., eds.) = Stars and stellar Systems Vol. IX, Univ. Chicago Press (1975). p. 409]. µ0 is independent of the type, but some individual galaxies are aberrant. Full circles: type I luminosity profiles; open circles: type II luminosity profiles, as explained in Fig. 3.

Figure 3 shows the radial luminosity distribution for three galaxies with different ratios of spherical and exponential components, and for comparison a R^1/4-distribution.

Figure 3. Radial luminosity distribution for NGC 4459 (type S0) M83 (Sc), and M33 (Scd). The R1/4 distribution is also shown [Freeman, K.C. in Galaxies and the Universe (Sandage, A., Sandage, M., & Kristian, J., eds.) = Stars and stellar Systems Vol. IX, Univ. Chicago Press (1975). p. 409].

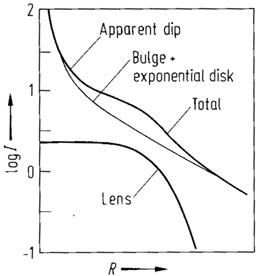
The luminosity profiles of high surface-brightness disks dip below the projected exponential component, see for instance M83 in Fig. 3. Freeman [Freeman, K.C. in Freeman, K.C. Observational Determination of the Overall Features. In Freeman, K., Larson, R.B., Tinsley, B. Galaxies, Sixth advanced course of the Swiss Society of Astronomy and Astrophysics (Martinet, L., Mayor, M., eds.), Geneva Observatory (1976) p. 1] supposes that those M83-like galaxies are systems with a lens component: the dip is the result of adding a flat lens component to the bulge and exponential components, as schematically shown in Fig. 4.

Figure 4. Possible explanation of the "dip" (M83 type, see Fig.3) by superposition of bulge-, exponential- and lens components [Freeman, K.C. in Freeman, K.C. Observational determination of the overall features. In Freeman, K., Larson, R.B., Tinsley, B. Galaxies, Sixth advanced course of the Swiss Society of Astronomy and Astrophysics (Martinet, L., Mayor, M., eds.), Geneva Observatory (1976) p. 1].