] or
log R = A + B
Reviews: [Galactic and Extragalactic Radio Astronomy (G.L. Verschuur, & K.I. Kellermann, eds.), Berlin, Springer (1988)].
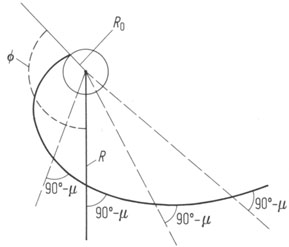
The density-wave spirals are usually well represented by logarithmic spirals with only slowly changing pitch angle [Kennicutt, R.C. Jr. Astron. J. 86 (1981) 1847] (see Fig. 5):
] or
log R = A + B
with x = tgµ(R); = winding angle; pitch angle µ being nearly constant.
Pitch angles in different galaxies vary between a few and about
30°; the change of the pitch angle within any system is at most
±4°
[Kennicutt, R.C. Jr. Astron. J. 86 (1981) 1847].
Material arms, on the other hand, possess a nearly hyperbolic form [Seiden, P.E., & Gerola, H. Astrophys. J. 233 (1979) 56]
= const .
Vrot(R) ,
dictated by the rotation curve of the galaxy.
|
Figure 5. The logarithmic spiral.
|
[Kennicutt, R.C. Jr. Astron. J. 86 (1981) 1847] investigated 113 objects
and considered two functions: logarithmic
spiral with constant pitch (i.e. linear in log R versus
) and hyperbolic spiral (i.e. linear
in R versus R) with
the result that neither logarithmic nor hyperbolic spirals accurately
represent the spiral arms; but, within the limitations set by arm
distortions, they may serve as adequate interpolation functions in
normal spiral systems. The question of the mathematical form is
irrelevant for the majority of real spiral arms.
Distribution of Pitch Angles:
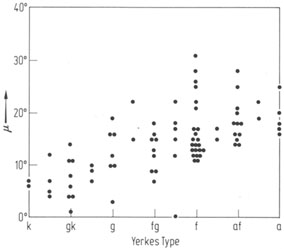
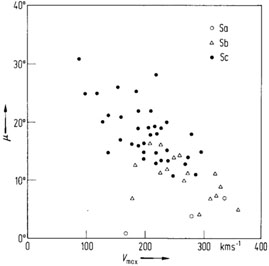
The pitch angles correlate weakly with the arm structures and with the bulge-to-disk ratio, i.e. the Hubble classification criteria are less closely coupled than thought previously [Roberts, M.S. Comments Astron. 6 (1976) 105]. But the maximum rotation velocity mix is well correlated with the arm pitch, suggesting that the shape of spiral pattern is mainly dictated by kinematic parameters, independent of the physical origin of the arms, Figs. 6 and 7.
|
Figure 6. The measured pitch angles vs. Yerkes-type galaxies [Kennicutt, R.C. Jr. Astron. J. 86 (1981) 1847]. |
|
Figure 7. Correlation between pitch angle µ and maximum rotational velocity Vmax for spiral galaxies [Kennicutt, R.C. Jr. Astron. J. 86 (1981) 1847]. |
In strongly barred galaxies the arms are systematically distorted. Observational constraints of driving mechanism for spiral density waves: [Kormendy, J., & Norman, C.A. Astrophys. J. 233 (1979) 539].
Galaxy Bars and Resonances to Drive the Spiral Structure:
Tidal Interaction as the Origin of Spiral Structure: