


3.2.4 The cosmological constant 
The cosmological constant  was introduced by
Einstein (1917). It
relates to the matter-density
was introduced by
Einstein (1917). It
relates to the matter-density  and is measured in units time-2. The
cosmological constant used by
Lemaître (1927)
is related to
matter-energy-density
and is measured in units time-2. The
cosmological constant used by
Lemaître (1927)
is related to
matter-energy-density  c2 and measured in units length-2,
it is the same as the cosmological constant used today.
c2 and measured in units length-2,
it is the same as the cosmological constant used today.
Einstein wrote:
``If it would then be certain, that the field equations which I have used so far, are the only ones in agreement with the postulate of the general theory of relativity, we must well conclude, that the theory of relativity does not admit the hypothesis of a spatial closure of the world.
. . . . We can, however, on the left-hand side of the field equations add the fundamental tensor gµv, multiplied with a presently unknown universal constant, without disturbing the general covariance; we put in lieu of the field equations
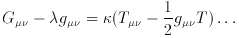
The newly introduced universal constant
thus determines the average distribution density
, which can remain in equilibrium, as well as the radius R of spherical space and its volume 2
2 R3.''
``The G-field is determined entirely by the masses of the bodies. Since mass and energy are the same according to the results of the special theory of relativity and the energy is formally described by the symmetrical energy tensor (Tµv) this means, that the G-field be entirely caused and expressed by the energy tensor of matter.''
Einstein calls this postulate 'Mach's principle':
``I have chosen the name Mach's principle because this principle is a generalization of Mach's requirement that inertia must be interpreted as the interaction of bodies.
According to [the originally proposed field equations] a G-field would be possible without any generating matter, contrary to Mach's principle.
But the postulate is fulfilled - according to my present understanding - by field equations which are obtained by adding the-term . . .
According to this equation a space-time continuum free from singularities with an everywhere disappearing energy tensor of matter seems not possible.``