


3.2.3 The current matter density of the universe  0 and its
normalized value
0 and its
normalized value  0
0
The matter density in space is of particular interest in relativistic universes, because it is closely related to the scale factor.
With the basic family of models introduced above (general relativity,
Friedmann-Robertson-Walker metric) and the assumption  = 0, and a
presently matter dominated universe (p0 = 0),
= 0, and a
presently matter dominated universe (p0 = 0),  0 relates in
simple ways
scale factor, deceleration parameter and Riemannian space curvature.
0 relates in
simple ways
scale factor, deceleration parameter and Riemannian space curvature.
The value of k is either +1, 0, -1 according to whether
It was from this formula, with k = 0, using the then accepted Hubble
constant of 500 km sec-1 Mpc-1 that Einstein and
de Sitter derived the value
in their famous paper of 1932.
Hubble (1934)
determined the density of luminous matter in space from
his counts of 44,000 nebulae with
with b = mass/luminosity ratio
log b is estimated from nearby systems to be of order unity, M is
estimated as -13.8 to -14.5. The result is given as
with an uncertainty probably less than 0.5 (units of
``The discussion, of course, ignores the existence of internebular
matter, the density of which, even in an optimal form, might be
several thousand times greater without introducing appreciable
absorption. Since absorption depends upon the state of material (the
density for large meteorites, for instance, might surpass that of the
galactic system without introducing appreciable obscuration), upper
limits can be assigned to the density of internebular space only from
dynamical considerations.''
An earlier value
(Hubble 1926) is
The matter density
For
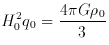
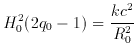
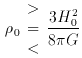
 0 = 4 x
10-28 g cm-3
0 = 4 x
10-28 g cm-3
M = absolute magnitude.
 0 = -29.8 or
0 = -29.8 or
 0 are g
cm-3):
0 are g
cm-3):
 0 = 1.5 x
10-31 g cm-3.
0 = 1.5 x
10-31 g cm-3.
 0 is frequently replaced by the dimensionless
quantity
0 is frequently replaced by the dimensionless
quantity  0 which
measures
0 which
measures  0
in terms of the Hubble constant,
according to the above formula:
0
in terms of the Hubble constant,
according to the above formula:
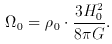
 = 0,
= 0,  0 = 1, corresponding to
the Euclidean universe (e.g.
Borner 1988).
0 = 1, corresponding to
the Euclidean universe (e.g.
Borner 1988).
 0 can be determined
directly from dynamical evidence, including the
`cosmic virial theorem', and from the abundance of elements formed in
the early universe.
0 can be determined
directly from dynamical evidence, including the
`cosmic virial theorem', and from the abundance of elements formed in
the early universe.