5.6 Selection
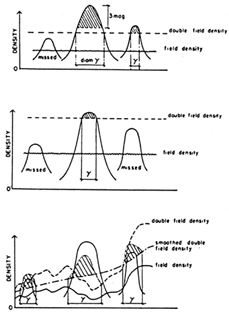
Selection effects arise because the observer sees different populations at different distances. With increasing distance only the absolutely brighter and larger galaxies are registered. The `Scott' effect (Scott 1957, 1962) states the same phenomenon with respect to cluster properties: at larger distances only rich and highly concentrated clusters appear above the sky background (Fig. 29). The combined effects of magnitude or diameter limits and the distribution functions of magnitude or diameter result in selection functions.
Selection effects are critical for sampling, especially when large population gradients exist across the sampling volume and when the measuring errors are large. The effect is referred to as Malmquist bias (1920). Malmquist introduced it originally in the context of stellar statistics, where he assumed the error distribution to be Gaussian. The Malmquist correction is used to compensate for the effect.
All correlations derived for magnitude- and diameter-limited samples suffer from severe Malmquist biases. Volume-limited samples are less influenced by population gradients. Corrections for the effects of error distribution must always be applied.
Other selection effects are introduced by the measuring procedures.
They result from the fact that most methods are more sensitive to
certain parameter values than to others. An example is the
preferential discovery of Ly 
-quasars (e.g.
Gericke 1988)
which is a
combined effect of favourable wavelength region and emission
characteristics of the line.
|
Figure 29. Visibility of clusters
(Scott 1962).
|