


6.1 The log  (z)-diagram
(z)-diagram
The first diagram used in observational cosmology appears to be the
log  (z)-diagram. In ist original version, it was not displayed, but
is described in detail by
Wirtz (1924):
(z)-diagram. In ist original version, it was not displayed, but
is described in detail by
Wirtz (1924):
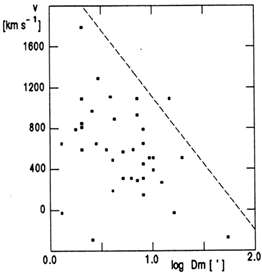
``When the different quantities v [velocity] versus lg Dm [diameter] are represented graphically, the diagram shows a V-shaped or triangular form from which one deduces the following facts: for the apparently small nebulae one finds smallest and largest v, the apparently largest nebulae have the smallest v, among the nebulae with small v one finds large and small objects, large nebulae with large v do not exist. From this one deduces, that the dispersion of the linear dimensions of the nebulae fills the triangular plane in such a way, that among the near nebulae absolutely small and large objects are visible while in the depth of space only the absolutely largest are subject to observing their radial motions. The progression between v and apparent Dm is reproduced best through the hypotenuse of the triangle enclosing all observed points, which follows the absolutely largest nebulae under the assumption that the giants among the nebulae have the same average extent at all distances.''
A reconstruction of the diagram is given in Fig. 30, using the data from papers quoted by Wirtz.
|
Figure 30. Reconstruction of Wirtz's original diagram. |