6.1. Lessons from Simple Models

The KIA (Kinematic Impulse Approximation) epicyclic models of Section 4 are strictly speaking applicable only to collisionless disk stars. Nonetheless, they can still provide some insight into the basic dynamics of the interstellar gas. The initial radial infall following the companion impact is essentially the same for both stars and gas elements. Different behaviors may begin in the compression of the first ring wave. Differences are inevitable if caustic edges are generated in the stellar wave, at least in the disk plane. The orbit crossing zone between these edges will collapse into a shock in the gas. However, Gerber's (1993) simulations showed that the disk may be sufficiently warped that the orbit crossing may not occur in a plane. The gas ring then looks surprisingly like the collisionless stellar ring. If the bulk of the gas is clumped in a relatively small number of giant molecular clouds of small cross section, they will also behave like stars in unwarped disks. Thus, the observation of shocks, or other dissipative effects, in rings would be an important discovery. Many first rings (see Figure 17) are too weak to form stellar caustics. Whether a (weak) shock forms in the gas or not depends on how closely the trajectories are squeezed compared with a typical cloud size, or how large are the cloud random motions within the ring.

In the case of caustic rings the approximations of Section 4 (and Appendix 2) could be generalized to the gas. Equation (4.15) essentially describes the center of the stellar orbit-crossing zone. Thus, it provides a reasonable first approximation to the trajectory of the gas shock. We can assume that gas elements follow collisionless trajectories until they hit the ring shock. Then, knowing their velocities and the shock velocity, the jump conditions can be applied to determine the (e.g., isothermal) postshock velocities. Behind the ring shock we can assume that the gas elements resume collisionless motion, until the equations describing this motion predict a second orbit-crossing zone, at which point the approximation can be repeated. The postshock collisionless trajectories in the gas will have different phases than the stellar trajectories, so subsequent shocks may not lie within the stellar ring. More likely, the gas motions will be damped, and there may be no subsequent shocks.

Star formation may be greatly enhanced even in modest rings which do not form global shocks. For example, consider how this would occur within the context of the classical gravitational instability theory. Kennicutt (1989) (also Struck-Marcell 1991; Taylor et al. 1994; and references therein) have argued that star formation in disks keeps the local gas surface density near a critical value, _cr. If the surface density is pushed above this critical value, a range of wavelengths becomes unstable to gravitational collapse. We can estimate a critical volume density corresponding to this surface density as

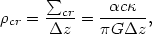
(6.1)

where c is the sound speed, is the local radial epicyclic frequency, z is the disk thickness, and is Kennicutt's empirical correction factor. The spherical free-fall time at this density is

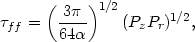
(6.2)

where P_r = 2 / is the radial epicyclic period, and P_z = z / c is the vertical acoustic period. With = 0.63 as in Kennicutt (1989) the constant in Equation (6.2) is about 0.5. Throughout much of the disk P_r and P_z are comparable, and thus, _ff is comparable to both. The time a typical gas element spends within a ring wave is also about P_r/2 (see Section 3). Thus, for any density enhancement of order a few or greater, there will be two or more growth times while the gas element passes through the wave.

This classical analysis assumes an initially uniform gas. If instead the gas is clumped into giant molecular clouds that are in approximate virial equilibrium, then the addition of mass or an increase of ambient pressure will lead to collapse on a shorter timescale. On the other hand, if star formation is the result of direct cloud collisions, these may not be significantly enhanced in weak waves. Thus, we would not expect much increase in the star formation. This is especially true if the star formation enhancement depends on the relative velocity of the colliding clouds. In weak waves, where orbit crossing is not predicted by the simple models, the relative velocities will be low. Thus, weak ring waves can provide a key test of the role of different star formation mechanisms.