APPENDIX 2: Simple Models for Asymmetric Stellar Ring-Like Waves

In this appendix we will briefly describe how the analytic kinematic, impulse approximation (KIA) model for caustic waves can be generalized to include waves that are not cylindrically symmetric. Because of the huge variety of such waves (see Sections 4.4 and 6) we cannot pursue this investigation very far in this review. However, nearly exactly symmetric collisions must be very rare, and in fact most known ring galaxies have some asymmetries. Thus, generalizing the theory is extremely important if it is to be tested against observations of real galaxies. Ring galaxy theory can serve as a prototype for studies of a wider set of interacting systems only to the degree that it can be readily generalized.

Analytic models for asymmetric caustic waves were explored in Struck-Marcell (1990), and a number of examples were presented for the case of a softened point-mass target and a Plummer potential companion galaxy. A more complete development of the SPM case, including an entirely analytic formula for the caustics as a function of time and the collision parameters is given in Wallin and Struck-Marcell (1994). This formalism was used by Donner et al. (1991) to produce semi-analytic models of waves produced in tidal interactions, and for the first time numerically solved the asymmetric caustic condition to determine the caustic edges. (Wallin (1989, 1990) independently investigated caustics in tidal tails using restricted three-body simulations.) In their comparison study of analytic models vs. N-body simulations Gerber and Lamb (1994) included the perturbation of the potential center of the target galaxy in KIA models. Their analytic models assumed a target potential with a flat rotation curve, and a Plummer potential for the companion.

In the following we will assume that the gravitational potential and the collisional potential amplitude are simple power-law functions of radius in the target disk. Once again, this greatly simplifies the algebra, making it easier to follow the basic ideas. Otherwise the discussion parallels that of Section II of Struck-Marcell (1990), and Wallin and Struck-Marcell (1994), with some modest generalizations.

We begin by considering the geometry of the impulsive perturbation, with the help of Figure A.1. Each panel shows a representative disk star at unperturbed radius q, and the companion impact point at radius r_*. R is the distance between the star and the impact point. The vector from the disk center to the impact point defines the x-direction, and is the azimuthal angle of the disk star relative to that axis. The law of sines relates the angle to by,

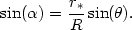
(A2.1)

In the first panel of Figure A.1 it is assumed that r_* << q, R, so || << 1. This limit is valid through most of the disk for slightly off-center collisions, and can be viewed as a perturbation of the symmetric collision case. As pointed out in the discussion of Equation (16) of Wallin and Struck-Marcell (1994) the analytic theory is considerably simplified in this limit.

The second panel is relevant to the inner disk for a slightly off-center impact, or the bulk of the disk for an impact at the edge, or outside of the disk. In this case r_* > q, but R can range from r_* - q to r_* + q. The magnitude of the angle is small in this case, but can range from - to . The former fact should simplify the analytic theory in this case, but this limit has not been much explored to date. This is unfortunate because that theory may be applicable not only to companions hiting at large angles to the disk, but also to all retrograde encounters. (In contrast to the prograde encounters which may not be sufficiently impulsive.)

Figure A1. Schematic illustrating definitions of various collision variables and parameters (see text). a) shows a case when the point of closest approach is outside the orbit of a representative disk. Part b) shows a case where the impact is inside the stellar orbit.

Let v be the (positive) magnitude of the velocity impulse at a point. The radial velocity perturbation v_r is always inward and negative in the nearly symmetric case. In the case of a large collisional offset v_r is positive and outward directed in half of the disk where the impact occurred, and negative inward in the other half. In both cases these in-plane components of the velocity impulse can be written

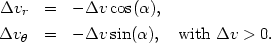
(A2.2)

v can be calculated as per the usual IA procedure (see e.g., Binney and Tremaine (1987), Section 7.2).

Generally, the disk plane will be tilted relative to the plane normal to the orbit at the moment of impact, and the angle of impact will not be perpendicular to the disk plane. Then the vertical impulse v_z will not be zero to first order as in symmetric collisions. Unfortunately, v_z will also not be easy to estimate accurately, nor will the modifications to v_r and v induced by this asymmetry. Although analytic estimates might be very helpful for interpreting simulations (in which such vertical effects are obvious), little work has been done in this area, and we will neglect these interesting effects here.

In the epicyclic approximation the post-collision orbit equations of a disk star are:

(A2.3)

The variables q, ₀ are the precollision radius and azimuth of the star, and q', are the post-collision guiding center and azimuth. The epicyclic and orbital frequencies at the new guiding center radius are ' = (q') and _cir(q'), respectively. The epicyclic phase of the star immediately after the collision is '.

The initial conditions at the moment of impact (t = 0) in the IA are:

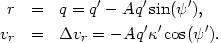
(A2.4)

These equations can be solved for the perturbation amplitude A and the phase ' in terms of v_r, q' and the precollision quantities, i.e.,

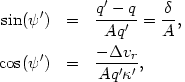
(A2.5)

where we have defined = (q' - q) / q', the fractional change of the guiding center radius. Squaring and adding these two equations, and using equation (A2.2), we obtain

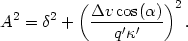
(A2.6)

The new guiding center radius q' can be obtained from the force balance equations for the guiding center orbit before and after the collision. Assuming a power-law rotation curve according to Equation (4.1) we have from Equation (4.2)

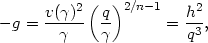
(A2.7)

where the specific angular momentum is h = qv. After the collision we have

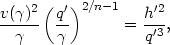
(A2.8)

with

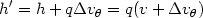
(A2.9)

in the IA. Combining these and solving for q' yields,

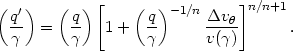
(A2.10)

Thus, in the case of a power-law potential we can solve explicitly for q'. This is not the case for most potentials.

Once v(q, ) is determined it can be substituted into Equation (A2.10), and then with the aid of Equations (A2.1) and (A2.2) we have q' in terms of unperturbed variables. This result can be used with Equation (4.4) in Equation (A2.6) to solve for A, and the in Equations (A2.5) for '. The expressions for q', ', A and ' can be substituted into (A2.3), yielding the desired expression for the post-collision stellar orbit in terms of the pre-collision values and the collisional parameters.

As a simple example, assume that the perturbation has a power-law dependence on the distance from impact, as in Equation (4.9), and write

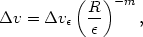
(A2.11)

with

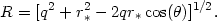
(A2.12)

A particularly simple case which we will examine in some detail is when m = 0, and n (i.e. a perfectly flat rotation curve in the primary). The perturbed guiding center is then

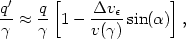
(A2.13)

using Equations (A2.10), (A2.11), and (A2.2). Also,

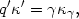
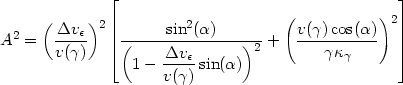
and

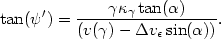
(A2.14)

These formulae can then be substituted into the first Equation of (A2.3) to obtain an explicit expression for the perturbed radius r. The fractional radial deviation (r - q')/q' depends only on t and functions of the angle . This is because v is constant in this case, and there are no other q' dependencies in the functions of Equation (A2.14).

The azimuthal dependence is equally simple since _cir = v/q', i.e.,

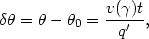
(A2.15)

This expression can be used to eliminate time from the radial equation,

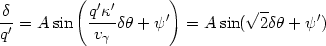
(A2.16)

which is the polar coordinate equation for the post-collision orbits. This r - orbit equation is equivalent to that of the curve called the Limacon of Pascal, which looks rather like an off-center circle with an inward pointing pucker or cusp.

Having determined the orbit equations, the next step (following the example of Section 4) is to calculate the caustic conditions, i.e., the boundaries of orbit crossing zones. In this case, the caustics are given by the zeros of the Jacobean determinant, i.e., the generalization of equation (4.12) is

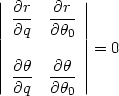
(A2.17)

Because of the simplicity of the expressions (A2.13) for q' in the power-law model, we have not specialized to the limit of small up to this point. A small radial amplitude approximation is implied when we adopt the epicyclic Equations (A2.13). However, this is not the same as assuming that the collisional perturbation is small. It is an approximation for the orbits in the primary galaxy which could, in principle, be replaced by a more exact form, e.g., in terms of elliptic functions. We could, in fact, proceed to work out the explicit analytic form for (A2.17) without further approximation. However, we will not pursue that here. At this point we will consider some limits.

The most important limit for present purposes is when the angle << 1, i.e., just slightly off-center collisions with r_* << q, R. It is also convenient (and reasonable) to assume A << 1, i.e., small amplitude perturbations. If instead of , we adopt the corotating variable = - _crit t, then the cross terms in Equation (A2.17) are both proportional to Asin(). Thus, the product of these terms can be neglected to first order, and Equation A2.17 becomes

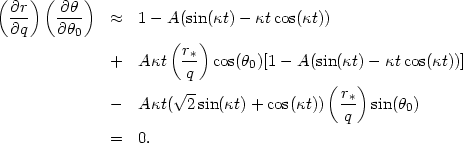
(A2.18)

Given the simple potential adopted, and the approximations made, this is probably the simplest formula describing collisional asymmetric caustic waves in galaxy disks. The first two terms alone describe the (inner and outer) caustic edges of a symmetric ring, as can be seen by taking r_* = 0, or comparing to Equation (4.14).

If we assume that the radius q and the phase t are constant on a caustic, but with r_* > 0, then (A2.18) is recognized as the equation of a circle whose center is offset from the origin. More realistically, at a fixed time the value of q on the caustic must vary with azimuth ₀ in order to solve (A2.18). If this variation is not too great then the caustic curves described by (A2.18) can be approximated by local circular arcs. Additionally it can be shown that Equation (A2.18) has banana or crescent-shaped solutions as well as complete circles. There are probably other, more complex waveform solutions as well. However, these have not yet been fully investigated.

We note again that it would also be interesting to study the analogous caustic equation in the retrograde encounter limit, i.e., where r_*, R >> q, and = - - << 1. This equation will be more complicated than (A2.18) because in this limit the cross terms of Equation (A2.17) are not negligible.