APPENDIX 1: Multiple Encounter Kinematics

In this Appendix the epicyclic KIA model is used to further examine the effects of a second symmetric collision described in Section 4.3. Specifically, immediately after the second collision, Equation (4.5) can be replaced with

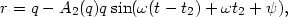
(A1.1)

where t₂ is the time of the second collision (with t = 0 at the first collision). The amplitude A₂ is defined through the velocity equation at time t₂,

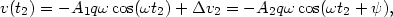
(A1.2)

where v₂ is the velocity impulse in the second collision, and the second equality defines A₂. Equations (A1.1) and (A1.2) can be combined to eliminate the phase ,

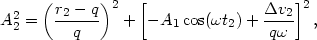
(A1.3)

with r₂ = r(t₂), the radius of the given star at the time of the second impact. This can be simplified using the relations

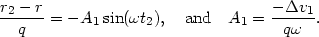
(A1.4)

Thus, we obtain

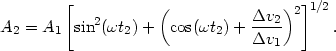
(A1.5)

The orbit equation then becomes

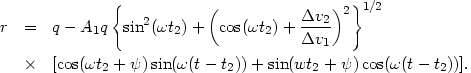
(A1.6)

In zones where the last term in the square brackets is small after the second impact, i.e., sin(t₂ + ) 0, Equation (A1.6) is essentially the same as Equation (4.5), but with a position-dependent amplitude.

In zones where the first term in the square brackets in Equation (A1.6) is small, i.e., cos(t₂ + ) 0, that equation is similar to Equation (4.5), but the perturbation term is off by a phase of / 2. As a result we expect a change in the morphology and rate of propagation at phases where there is a change of dominance from one term to the other. The models confirm-that the rings do not propagate as rapidly outward following the second impact as they did during the first.

When cos(t₂) > 1, all of the terms in Equation (A1.5) add, and the wave amplitude will be relatively large (unless cos(t₂ + ) is small). When cos(t₂) < 1 the last two terms on the rights-hand-side of Equation (A1.5) will tend to cancel, resulting in weak waves in that region. Indeed if the phase t₂ is such that sin(t₂) 0, then A₂ 0, i.e., the second perturbation can essentially cancel the first. Such trajectories are seen in the models. If the amplitude of nearby trajectories is large enough they can cross the A₂ 0 trajectory. The result is a ring that does not propagate outward, but its width varies with time. Though it will be affected by stellar diffusion, such a stationary ring could be long-lived. Because their locations depend on the details of the collisions as well as the disk structure, they will in general have no relation to classical Lindblad resonances.