Copyright © 1988 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1988. 26:
631-86 Copyright © 1988 by Annual Reviews. All rights reserved |
The increase of correlation strength with richness implies that rich,
luminous systems are more strongly clustered, at a given separation,
than poorer systems. The power law of the correlation functions is
also observed to be identical in the various systems studied. Either
initial conditions, or subsequent evolution, may be responsible for
the observed phenomena. Since the observed correlation functions
follow the same power law (r-1.8), the effect of
increased correlation
strength with richness (at a given separation) can also be expressed
as a scale shift in the correlation functions
(Szalay & Schramm
1985).
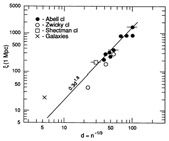
In Figure 12 I plot the amplitude of the
correlation functions
of the various systems (galaxies, poor and rich clusters,
superclusters) as a function of the mean separation of objects in the
sample, d (see
Bahcall & Burgett
1986,
Bahcall 1987).
The mean separation is related to the mean spatial density of objects
in the sample, n, through
d = n-1/3. For example, the mean separation of
galaxies is about 5 Mpc, while the mean separations of R
 1 and R
1 and R
 2
clusters are, respectively, about 50 Mpc and 70 Mpc.
2
clusters are, respectively, about 50 Mpc and 70 Mpc.
It is apparent from Figure 12 that the correlation strength increases with the sample's mean separation. Moreover, a dimensionless correlation function normalized to the sample's mean separation d appears to yield a constant, universal function for nearly all the systems studied (some enhancement is required for galaxies, as described below). This universal dimensionless correlation function has the form
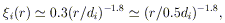
| (16) |
where the index i refers to the system being considered, and
di is its
mean separation. Relation 16 implies a universal dimensionless
correlation amplitude of ~ 0.3, and, equivalently, a universal
correlation scale of
r0  0.5di. The correlation function of galaxies
is stronger than that expressed by relation (16) by a factor of about
four (Figure 12). The universality of the
correlation function
suggests a scale-invariant clustering process
(Szalay & Schramm
1985).
The stronger dimensionless galaxy correlations may imply gravitational
enhancement on smaller scales. If a nonlinear process, other than
gravity, participates in galaxy formation, and this process is
scale-invariant, the created structure will have a single power-law
correlation function, the slope of which
(
0.5di. The correlation function of galaxies
is stronger than that expressed by relation (16) by a factor of about
four (Figure 12). The universality of the
correlation function
suggests a scale-invariant clustering process
(Szalay & Schramm
1985).
The stronger dimensionless galaxy correlations may imply gravitational
enhancement on smaller scales. If a nonlinear process, other than
gravity, participates in galaxy formation, and this process is
scale-invariant, the created structure will have a single power-law
correlation function, the slope of which
( ) is related to the
geometry of the structure (i.e. its fractal dimension
) is related to the
geometry of the structure (i.e. its fractal dimension
 ). The latter
is related to the correlation function slope via
). The latter
is related to the correlation function slope via
 =
=
 - 3 (see,
e.g. Mandelbrot 1982).
The fractal dimension of the universal
structure implied by the above data is therefore
- 3 (see,
e.g. Mandelbrot 1982).
The fractal dimension of the universal
structure implied by the above data is therefore

 1.2. Small-scale
gravitational clustering may break the scale invariance and increase
the dimensionless correlation amplitude for galaxies.
1.2. Small-scale
gravitational clustering may break the scale invariance and increase
the dimensionless correlation amplitude for galaxies.
|
Figure 12. The dependence of the correlation function on the mean separation of objects in the system. The results are for clusters from different catalogs (Abell, Zwicky, and Shectman, as indicated by the symbols), determined by different investigators for samples of different mean densities (i.e. mean separations) (Section 3). The correlation strengths for galaxies and superclusters are also included. The solid line represents a d1.8 dependence (e.g. Szalay & Schramm 1985, Bahcall & Burgett 1986). |
We do not know yet what physical process can create a
scale-invariant structure with

 1.2. An innovative suggestion
involves cosmic strings as the primary agent in the formation of
galaxies and clusters; this model appears to create such a
scale-invariant infrastructure
(Turok 1985).
The model yields a
scale-invariant correlation function similar to that observed, with a
power law of -2 (as implied by one-dimensional "string" structures
with fractal dimension of unity). More detailed calculations with
string models are currently being carried out by several investigators
(Section 9).
1.2. An innovative suggestion
involves cosmic strings as the primary agent in the formation of
galaxies and clusters; this model appears to create such a
scale-invariant infrastructure
(Turok 1985).
The model yields a
scale-invariant correlation function similar to that observed, with a
power law of -2 (as implied by one-dimensional "string" structures
with fractal dimension of unity). More detailed calculations with
string models are currently being carried out by several investigators
(Section 9).