Annu. Rev. Astron. Astrophys. 1988. 26: 631-86 Copyright © 1988 by Annual Reviews. All rights reserved

6. SUPERCLUSTERS AND VOIDS

In this section I consider the superclustering of clusters and discuss the identification and properties of individual superclusters. This approach complements the statistical studies of correlation functions, providing specific information about type, shape, structure, and content of superclusters. For a recent review paper on superclusters, see Oort (1983). A review of voids is presented in this volume by Rood (1988).

6.1. Supercluster Catalogs

In order to investigate the properties of the large-scale clustering of clusters, a complete, well-defined catalog of superclusters - defined as clusters of clusters of galaxies - is required. Early lists of superclusters (e.g. Abell 1961, Rood 1976, Murray et al 1978) used the projected distribution of rich Abell clusters plus estimated cluster redshifts (from Abell's magnitudes of the tenth brightest cluster galaxy), since very few redshift data were available. (The latter were used by Rood 1976.) Later on, Thuan (1980) used measured redshifts of the 77 nearest Abell clusters, with a single selection parameter; no comparisons with random catalogs were available. More recently, Bahcall & Soneira (1984) (hereinafter BS84) constructed a supercluster catalog to z 0.08 using the complete redshift sample of 104 nearby Abell clusters (D 4, z 0.1) described in Section 2 and an objective selection criterion of a spatial density enhancement. I describe below the main properties of these catalogs.

In the BS84 catalog, all volumes of space with a spatial density of clusters f times larger than the mean cluster density are identified as superclusters for a specified value of f. The superclusters densities are therefore given by

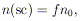
(18)

where n(sc) is the spatial density of clusters in the supercluster, and n₀ is the mean cluster density in the sample. The supercluster selection process was repeated for various overdensity values f, from f = 10 to f = 400, yielding specific supercluster catalogs for each f value. The higher over-density values identify the dense cores of superclusters; lower f values represent superclusters with lower densities and include the outskirts of high-density superclusters. The supercluster boundaries clearly do not set strict physical limits on the superclusters but rather define volumes of various levels of overdensities. The procedure was carried out for the redshift sample of 104 clusters of richness R 1, as well as for the larger redshift sample of 175 R 0 clusters.

A map of the supercluster catalog for the R 0 sample is presented in Figure 15. Additional supercluster maps (e.g. the R 1 sample), as well as a listing of the supercluster catalog itself and its member clusters for each of several f values, are given in BS84. A total of 16 superclusters are cataloged for R 1 and f = 20, and 26 superclusters for R 0 and f = 20.

Figure 15. Projected area map of the northern (top) and southern (bottom) clusters and superclusters in the D 4, R 0 Abell sample (BS84). Outer contour is |b| = 30°; inner contour is the completeness of the sample. The Galactic poles are at the respective centers of these polar maps. Longitude l is 0° at the west and increases clockwise. The density contours represent the three-dimensional density enhancement of the superclusters, from f = 20 to f = 400 (Section 6). The Corona Borealis supercluster is at ~ 15h + 30°; Hercules is at ~ 16h + 15°; Ursa Major is at ~ 11.5h + 55°. For a map of the R 1 superclusters, see BS84.

Some global properties of the Bahcall-Soneira superclusters are summarized in Table 2. The number of clusters per supercluster varies from 2 to 15 for the f = 20 superclusters and reduces to a value of 2 to 3 clusters per f = 400 supercluster. The average number of clusters per supercluster is approximately three. The superclusters contain a large fraction of all clusters; this fraction, F_cl(sc), is 54% at f = 20 and reduces to 16% at f = 400. Comparisons with random catalogs show that these fractions are considerably higher than those expected by chance (Figure 16). This indicates that most of the high overdensity superclusters are real physical systems of the largest scale yet observed. The linear size of the largest observed superclusters are 100h^-1 Mpc (at f = 20; e.g. the Corona Borealis supercluster at ~ 15^h + 30°). Elongated structures are suggested in these cases. The fractional volume of space occupied by the superclusters is, however, very small; it is ~ 3% at f = 20 and decreases rapidly with increasing f.

Table 2. Global properties of superclusters ^a

	f
Property	20	40	100	400
Nsc	16	12	11	7
ncl/sc	2-15	2-7	2-7	2-3
Rmax (Mpc)	145	36	36	13
< rx> (Mpc)	27.1	7.6	7.6	4.5
< Rz> (Mpc)	28.6	14.5	13.5	4.5
Fcl(sc)	0.54	0.34	0.30	0.16
Vsc/V	0.03	0.008	0.003	0.0004
a The quantities listed are for the R 1 sample.Notation: Nsc, total number of superclusters; ncl/sc, number of R 1 clusters per supercluster (i.e. supercluster richness); Rmax linear size of the largest supercluster; < Rx> and < Rz>, mean projected (one-dimensional) and redshift separations (in Mpc) of all cluster pairs in the superclusters; Fcl(sc), fraction of all R 1 clusters that belong in superclusters; Vsc/V, fractional volume of space occupied by the superclusters.

Figure 16. The Fraction of all R 1 clusters that are supercluster members as a function of the supercluster density enhancement f (BS84). Crosses represent the data; dots represent the ensemble average of 100 random catalogs. The l error bars are shown for the random points. The curves are power-law fits for f >> 1 (Section 6).

Thuan (1980) constructed a supercluster catalog from the nearest 77 Abell clusters by finding all cluster neighbors within a given separation of 65h^-1 Mpc. While the selection criteria differ somewhat from those of BS84, there is general consistency between the catalogs.

Rood (1976) determined the superclustering of the nearest 27 Abell clusters using the clusters' measured redshifts and the criterion of having at least one cluster neighbor within 25h^-1 Mpc. In the region of overlap, a general consistency exists among the Rood. Thuan, and Bahcall & Soneira catalogs. Kalinkov et al. (1984) determined the superclustering of the nearby Abell clusters using measured as well as estimated redshifts. Batuski & Burns (1985b) used measured as well as estimated redshifts (from Abell's m₁₀ magnitude) for all Abell clusters in order to identify a large list of candidate superclusters. Further redshift measurements are required before the reality of these suggested superclusters can be determined

6.2. The Multiplicity Function of Superclusters

Approximately one half of all rich clusters are observed to be members of superclusters (Section 6.1). The frequency distribution of clusters among superclusters of different richnesses, n_cl/sc (where n_cl/sc is the number of clusters in a supercluster), is the multiplicity function of the clusters, F_cl(n_cl/sc). This multiplicity function was determined by BS84 for their complete sample of superclusters (Section 6.1) and compared with the multiplicity function expected from random samples.

The multiplicity function is presented in Figure 17, showing the fraction of clusters that are members of superclusters of any given richness. The frequency distributions are plotted for different values of density enhancement selection value f, from f = 10 to 400, for both the data and the average of 100 random cluster catalogs. Figure 17 shows that the observed and random catalogs yield different distributions. The fraction F_cl for the random catalog falls off smoothly and steeply with increasing richness (for f 10); thus, the random catalogs have essentially no power at large richness. The observed superclusters have systems with more members than seen in the random catalogs for all f 10. The observed high-richness superclusters (high n_cl/sc) appear to grow rapidly (in richness and size) as f decreases. As these richest, largest scale structures grow, a gap of medium-richness superclusters appears to be rapidly forming (Figure 17). Neither the gap nor the related largest scale structure exists in the random catalogs.

Figure 17. The frequency distribution of R 1 clusters that are members of superclusters of various richnesses, ncl/sc (Section 6). (The first bin, ncl/sc = 1, refers to single clusters; bins ncl/sc = 2, 3, etc., represent superclusters with two, three, etc., cluster members.) The distributions are given for four different density enhancements f. The histogram represents the observed catalog; the dashed line is the average of 100 random catalogs (BS84).

6.3. Superclusters Surrounding Galaxy Voids

The BS84 supercluster catalog was used by Bahcall & Soneira (1982a) to study the area around the large (~ 60h^-1 Mpc diameter) void of galaxies in Bootes that was detected by Kirshner et al. (1981). The largest, densest superclusters are located near and around the area devoid of galaxies. The Bootes void, at approximately 14.5^h + 50°, is located near superclusters BS 12 and BS 15+16 (~ 100h^-1 Mpc away in projection; see Figure 15 and BS84). In addition, the overdensity of galaxies observed by Kirshner et al. (1981) on both redshift sides of the void, at z 0.03 and z 0.08 (Figure 18), coincides in redshift space with these nearby dense superclusters: BS 15 + 16 (Hercules supercluster) at z 0.03, and BS 12 (Corona Borealis supercluster) at z 0.08 (Figure 18). This suggests that the large superclusters surround the galaxy void, and that the tails of their galaxy distributions account for the neighboring overdensities observed 100h^-1 Mpc away by Kirshner et al. This connection provides another indication of long tails to rich superclusters.

Previous observational evidence (Gregory & Thompson 1978, Gregory et al. 1981, Chincarini et al. 1981), together with these results as well as more recent redshift surveys (Giovanelli et al. 1986, de Lapparant et al. 1986, da Costa et al. 1988), suggests that galaxy voids may generally be associated with surrounding galaxy excesses: the bigger the void, the stronger may be the related excess.

Figure 18. The frequency distribution of Abell clusters, Ncl, and galaxies in the Bootes direction (Kirshner et al. 1981), Nglx as a function of redshift. The Bootes void at z 0.04 - 0.06 and the surrounding galaxy excess at z 0.03 and 0.08 are apparent in (b). The D 4 cluster distribution in the north (a) shows superclustering at the same redshifts as seen in the galaxy excess above (0.03 and 0.08); this superclustering originates close ( 100h-1 Mpc) to the Bootes void (c, d) at the Hercules supercluster (z 0.03 ) and Corona Borealis (z 0.08). The tails of these superclusters appear to extend ~ 100h-1 Mpc in size and cause the galaxy excess observed around the Bootes void (b) (Bahcall & Soneira 1982a).

6.4. Voids of Rich Clusters

A huge void of cataloged nearby rich clusters of galaxies was suggested by Bahcall & Soneira (1982b) in the complete D 4 Abell sample discussed above. The void, located at l ~ 180°, b ~ 30 - 50°, is in the approximate redshift range of z 0.03 - 0.08, and it extends ~ 100° across the sky (i.e. ~ 300h^-1 Mpc). Its projected area is completely devoid of nearby - but not distant - rich clusters (R 1). The void does not appear to be caused by absorption in the Galaxy. If this apparent void in nearby rich clusters is real, it subtends a volume of more than 10⁶h^-3 Mpc³. Simulations with 100 random catalogs indicate that the probability of finding such a large void by chance is 10^-2 [Bahcall & Soneira 1982b; see, however, Politzer & Preskill (1986), who estimate a higher random probability].

Recent work by Lipovetsky (1987), who studied the space distribution of Markarian galaxies from the First Byurakan Survey (using a UV excess technique), indicates a large void in the galaxy distribution in exactly the same rich-cluster void region as was suggested by Bahcall & Soneira (1982b). The cluster catalog of Shectman (1985), which lists poorer clusters than Abell's (Section 2), also has a significant underdensity of poor clusters in this region. Shectman finds 14 poor clusters in this area compared with an expected number of 32 (based on the density of clusters in the same Galactic latitude bin but different longitude). Other large voids in the distribution of rich clusters were suggested by Batuski & Burns (1985b), but no comparisons with random distributions were made. More recently, Huchra (1988) suggested the existence of similar huge voids of clusters using redshift observations of a deep (z 0.2) subsample of Abell clusters.

Proving that a void exists in a sparse distribution of rich clusters is obviously difficult and can be achieved only for very large regions devoid of clusters. On the other hand, if clusters are observed to be overdense on supercluster scales (~ 100h^-1 Mpc), it is reasonable to expect that similar underdense regions exist also.