Annu. Rev. Astron. Astrophys. 1988. 26: 631-86 Copyright © 1988 by Annual Reviews. All rights reserved

8. PECULIAR MOTION OF CLUSTERS

The discussion in the previous sections summarizes evidence for the existence of structures on the scale of ~ 10 - 150h^-1 Mpc. A question of critical importance is what are the velocity fields in these structures. Peculiar velocities of clusters on these scales may indicate the existence of large amounts of (dark) matter and are of fundamental importance for models of galaxy and structure formation. Early discussions of possible peculiar velocities among clusters in superclusters were presented by Abell (1961) and Noonan (1977). Noonan observed a tendency of clusters with neighboring Abell clusters to have a greater scatter on the Hubble diagram, which was interpreted as a gravitational perturbation on the cluster redshifts due to the neighboring clusters. More recently, Bahcall et al. (1986) used the complete redshift sample of D 4 rich Abell clusters (Section 2) to study the possible existence of peculiar motion and/or structural anisotropy on large scales. They find strong broadening in the redshift distribution that corresponds to a cluster velocity of ~ 10³ km s^-1. These findings are summarized below.

Recent observations of galaxy peculiar velocities on large scales (Rubin et al. 1976, Dressler et al. 1987, Aaronson & Mould 1988) indicate motion, or a bulk flow, on the scale of approximately 60h^-1 Mpc toward a large mass concentration; the indicated motion is about 600 km s^-1 relative to the microwave background. Yahil (1988) and Strauss & Davis (1988) used the IRAS galaxy survey to trace the gravitational field over a comparable volume around us. They suggest that velocity flows exist mostly on smaller scales around various local density enhancements (superclusters).

8.1. Redshift Elongation: The "Finger-of God" Effect

The distribution in space of the D 4 redshift sample of Abell clusters was studied by Bahcall et al. (1986) by separating the three-dimensional distribution into its components along the line-of-sight (redshift) axis and the perpendicular axes projected on the sky. All clusters were assumed to be located at their Hubble distances as indicated by their redshifts, and their pair separations (in megaparsecs) were determined in the three components. A scatter-diagram of the cluster pair separations in the redshift (z) direction (R_z) versus their separations in or (R or R) was then determined.

If all clusters were located at their Hubble distances with negligible peculiar motion, and if the sample was not dominated by elongated structures in a given direction, a symmetric scatter diagram should be observed. If a large peculiar velocity exists among clusters, it would manifest itself as an elongated distribution along the z-direction in the R_z - R and R_z - R diagrams. This elongation, often called the "Finger-of-God" effect, is normally interpreted as peculiar motion. However, the effect may also be caused by geometrically elongated structures if they dominate the sample (with elongation in the z-direction; see below).

The results are presented in Figures 19 to 21. The scatter diagrams are plotted in Figure 19 for both the R 0 and R 1 samples. Frequency distributions representing these diagrams are presented in Figure 21. A strong and systematic elongation in the z-direction exists in all the real samples studied. Scatter diagrams for sets of random catalogs do not exhibit any conspicuous elongation (Figure 20), as expected; a symmetric distribution in all directions is observed. As an additional test, Bahcall et al. (1986) also determined the scatter diagrams in the projected plane R - R, of the cluster sample (Figure 20). Again, as expected, a symmetric distribution is observed in this plane. These tests strengthen the conclusion that the observed elongation is real. The effect of elongation is strong; statistically, it corresponds to approximately 8 in a single sample (assuming, for illustrative simplicity, Gaussian statistics). It is therefore unlikely that the observed redshift elongation is a chance fluctuation. The effect becomes more apparent in the larger R 0 sample; this increase is expected if the effect is real.

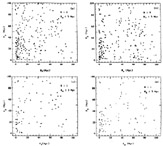
Figure 19. Scatter diagrams of Abell cluster pair separations (in megaparsecs) in the Rz - R and Rz - R planes (Bahcall et al. 1986). (The pair separations along the third axis, perpendicular to each plane, are limited to 5 Mpc.) All cluster pairs with a total spatial separation 100 Mpc are included. Parts (a, b) and (c, d) represent, respectively, the R 0 and R 1 richness samples. The elongation in the redshift direction is apparent in all cases (see Section 8).

A similar effect was observed by BS83 in their comparison between the cluster correlation function in the redshift and spatial directions. A broadening in the redshift direction was observed in that study, similar to the present findings. The elongation is unlikely to be caused by background/foreground contamination of galaxies and clusters (e.g. Sutherland 1988), since this would yield an excess of pairs at any R_z separation, as well as any R or R, rather than the excess (i.e. broadening) observed specifically at small separations ( 0.015). The effect is also much larger than either the uncertainties in the redshift measurements or the uncertainties caused by the internal velocity dispersion within the clusters (see below).

Figure 20. Same as Figure 19 but for typical random distribution of clusters (a, b), and for the projected distribution (i.e. R - R plane) of the actual cluster samples (c, d). No elongation is expected in either case, and none is observed. The clustering of clusters is apparent in the data sample of (c, d).

Figure 21. Histograms representing the distribution of pairs along the redshift, Rz, and projected, R and R, directions (as determined from the scatter diagrams) are shown for the R 0 (a) and R 1 (b) samples. The number of cluster pairs as a function of projected separation, N(R) or N(R), is represented by the solid histogram. The number of cluster pairs in the redshift direction, N(Rz), is represented by the dashed histogram. The solid curve represents a convolution of the projected distribution [N(R) or N(R)] with a Gaussian of 2000 km s-1 width. This convolved profile is in general agreement with the broadened distribution observed in the redshift direction, N(Rz).

The above value for the velocity width includes all contributions to the broadening effect, such as redshift measuring uncertainty and possible deviations from the true cluster redshift due to individual galaxy velocities in the clusters. Redshift measuring uncertainties are negligible compared with the 2000 km s^-1 velocity width observed. The effect of peculiar motion within the clusters (for those clusters that have only a small number of measured galaxy redshifts) was estimated by comparing cluster redshifts from the current sample with those obtained using a larger number of measured galaxy redshifts, when available. For the latter study (Bahcall et al. 1986), the redshift catalogs of Sarazin et al. (1982) and Fetisova (1981) were used. A root-mean-square deviation for these cluster redshifts of approximately 300 km s^-1 is observed due to the above effect. This value is reasonable considering that the full velocity dispersion in clusters is typically ~ 1000 km s^-1, and that the redshifts measured are for the brightest centrally located galaxies; these galaxies are generally close to the central velocity of the cluster. Subtracting quadratically a possible deviation of 300 2 km s^-1 from the observed 2000 km s^-1 yields 1950 km s^-1, i.e. a negligible change. Even if we assume, conservatively, ~ 700 km s^-1 for the internal broadening, the net cluster pair velocity is still 1740 km s^-1. Thus, a considerable elongation effect of approximately 10³ km s^-1 per cluster remains after correction for internal motion.

The observed elongation may be caused by either peculiar motion of clusters or a true geometrical elongation of superclusters. These are briefly discussed below.

8.2. Explanations of the Redshift Elongation

8.2.1   PECULIAR VELOCITY AMONG CLUSTERS   If the observed elongation is caused primarily by peculiar motion of clusters in superclusters, the net cluster pair motion in the line of sight is approximately 1700 km s^-1, or, equivalently, about 1200 km s^-1 for single cluster motion. Most of this effect arises in the central parts of the rich superclusters. A large peculiar velocity could be caused by the gravitational potential of the superclusters or by nongravitational effects such as explosions.

To estimate a supercluster mass that may support this velocity, a typical supercluster size of ~ 25h^-1 Mpc (= cluster correlation scale length) is used and the virial relation M v²r is assumed. This yields a typical supercluster mass of

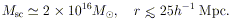
(19)

This mass is comparable to the mass of ~ 20 rich clusters, while typically only ~ 3 - 5 rich clusters are members of a supercluster. Even when the luminous tails of clusters are accounted for, the result may still suggest an excess of dark matter in superclusters as compared with clusters. Using an observed luminosity and/or density profile of r^-3 or r^-2.5 around a rich cluster, we estimate an M/L for superclusters that is typically twice that of rich clusters, i.e. M/L ~ 500.

Redshift observations of two individual higher redshift superclusters (Ciardullo et al. 1983) appear to indicate a much lower velocity for the superclusters than suggested even by a free expansion. This suggests, for these two systems, either a flat face-on geometry of the superclusters (consistent with Section 8.2.2) or a slow-down of the initial expansion due to the supercluster mass. In either case, it is likely that individual superclusters are at different stages of their evolution as well as at different observed orientations. The Corona Borealis supercluster (Bahcall et al. 1986) appears to show a redshift elongation in the distribution of both its clusters and the galaxies.

8.2.2   GEOMETRICAL ELONGATION OF SUPERCLUSTERS   The elongation observed in the scatter diagrams may also be caused, at least partially, by a geometrical elongation of superclusters. If the most prominent superclusters are elongated in the line-of-sight direction, an apparent elongation in the distribution of pair separation along this axis may result. I discuss below an observational test to distinguish between peculiar velocity and geometrical elongation of large-scale structures.

8.2.3   TESTS TO DISTINGUISH BETWEEN PECULIAR VELOCITY AND GEOMETRICAL ELONGATION   If the observed redshift elongation is caused by geometrical elongation, cluster redshifts should be correlated with the magnitude of their standard galaxies, following Hubble's law. No such magnitude-redshift correlation should be present if the effect is entirely due to peculiar velocity. More generally, an independent distance indicator (such as the magnitude of the brightest cluster galaxy or Tully-Fisher-type relations) could be used to determine the actual distances to the clusters and thus to interpret the origin of the observed redshift broadening (by comparing the actual distances with the observed redshifts).

The dependence of galaxy magnitudes on redshift in the close cluster pairs was studied by Bahcall et al. (1986). The magnitude of the brightest galaxy in each cluster, m₁^c, corrected for the cluster morphological type and richness as given by Hoessel et al. (1980), was used as a distance indicator. If the observed redshift elongation is caused by geometrical anisotropy, a proper (Hubble) correlation of m₁^c with z is expected within individual superclusters. This correlation should not exist if peculiar velocity is the cause of the observed elongation. The expected magnitude difference for a cluster pair with a redshift separation of about 0.01-0.015, assuming Hubble distances, is ~ 0.3 to 0.5 mag (depending on z). This difference is large enough to be measured with accurate observations of standard galaxy magnitudes. A marginal m₁^c dependence was found (Bahcall et al. 1986) for some individual superclusters, suggesting that at least some of the redshift broadening observed may be due to geometrical elongation of the large structures. Increased accuracy and greater statistics for galaxy magnitudes may clarify the significance of the results. It is possible that both geometrical elongation and peculiar velocity of clusters contribute to the observed redshift broadening. Other distance indicators, such as Tully-Fisher or Faber-Jackson relations, should also be applied to the problem in order to help distinguish between peculiar motion and geometry. Recently, comparable velocities of ~ 10³ km s^-1 between some cluster pairs were also suggested by Mould (1988) and Burstein (1988) using actual distance indicators of galaxies.