6.1. Models

Efforts to predict the intensity and spectrum of the EBL by Partridge & Peebles (1967) and Harwit (1970) began with the intent of constraining cosmology and galaxy evolution. Tinsley (1977, 1978) developed the first detailed models of the EBL explicitly incorporating stellar initial mass functions (IMFs), star formation efficiencies, and stellar evolution. Most subsequent models of the EBL have focused on integrated galaxy luminosity functions with redshift-dependent parameterization, with particular attention paid to dwarf and low surface brightness galaxies (see discussions in Guiderdoni & Rocca-Volmerange 1990, Yoshii & Takahara 1988, and Väisänen 1996).

More recent efforts have focused on painting a detailed picture of star formation history and chemical enrichment based on the evolution of resolved sources. The evolution of the UV luminosity density can be measured directly from galaxy redshift surveys (e.g., Lilly et al. 1996, Treyer et al. 1998, Cowie et al. 1999, Steidel et al. 1999, Sullivan et al. 2000), from which the star formation rate with redshift, _*(z), can be inferred for an assumed stellar IMF. The mean properties of QSO absorption systems with redshift can also be used to infer _*(z), either based on the decrease in HIcolumn density with decreasing redshift (under the assumption that the disappearing HIis being converted into stars) or based on the evolution in metal abundance for an assumed IMF and corresponding metal yield (e.g., Pettini et al. 1994; Lanzetta, Wolfe, & Turnsheck 1995; Pei & Fall 1995). Estimates of the star formation rate at high redshift have also come from estimates of the flux required to produce the proximity effect around quasars (e.g., Gunn & Peterson 1965, Tinsley 1972, Miralda-Escude & Ostriker 1990). Using these constraints, the full spectrum of the EBL can then be predicted from the integrated flux of the stellar populations over time.

Unfortunately, all methods for estimating _*(z) contain significant uncertainties. The star formation rate deduced from the rest-frame UV luminosity density is very sensitive to the fraction of high mass stars in the stellar initial mass function (IMF) and can vary by factors of 2-3 depending on the value chosen for the low mass cut off (see Leitherer 1999, Meader 1992). Aside from the large uncertainties in the measured UV luminosity density due to incompleteness, resolved sources at high redshift are biased towards objects with dense star formation and may therefore paint an incomplete picture of the high-z universe. Also, large corrections for extinction due to dust must be applied to convert an observed UV luminosity density into a star formation rate (Calzetti 1997).

The SFR inferred from QSO absorption systems, whether from consumption of HIor increasing metal abundance, is also subject to a number of uncertainties. In all cases, samples may be biased against the systems with the most star formation, dust, and metals: dusty foreground absorbers will obscure background QSOs, making the foreground systems more difficult to study. In addition, large scale outflows, a common feature of low-redshift starburst galaxies, have recently been identified in the high-redshift rapidly star-forming Lyman break galaxies (Pettini et al. 2000), suggesting that changes in the apparent gas and metal content of such systems with redshift may not have a simple relationship to _*(z) and the metal production rate. The mass loss rate in one such galaxy appears to be as large as the star formation rate, and the recent evidence for CIVin Ly- forest systems with very low HI column densities ( × 10¹⁴ cm^-2) suggests that dilution of metals over large volumes may cause underestimates in the apparent star formation rate derived from absorption line studies (see Ellison et al. 1999, Pagel 1999, Pettini 1999 and references therein).

Finally, regarding the predicted spectrum of the EBL, the efforts of Fall, Charlot, & Pei (1996) and Pei, Fall, & Hauser (1998) emphasize the need for a realistic distribution of dust temperatures in order to obtain a realistic near-IR spectrum.

With these considerations in mind, we have adopted an empirically motivated model of the spectral shape of the EBL from Dwek et al. (1998, D98). This model is based on _*(z) as deduced from UV-optical redshift surveys and includes explicit corrections for dust extinction and re-radiation based on empirical estimates of extinction and dust temperature distributions at z = 0. The comoving luminosity density can then be expressed explicitly as the sum of the unattenuated stellar emission, _s(, z), and the dust emission per unit comoving volume, _d(, z). Equation 1 then becomes

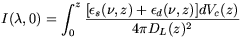
(3)

D98 estimate the ratio _d(, 0) / _s(, 0) by comparing the UV-optical luminosity functions of optically detected galaxies with IR luminosity function of IRAS selected sources. Using values of = (1.30±0.7) × 10⁸ L Mpc^-3 for the local stellar luminosity density at 0.1-10µm and = 0.53 × 10⁸ L Mpc^-3 for the integrated luminosity density of IRAS sources, Dwek et al. obtain _d(, 0) / _s(, 0) ~ 0.3. The redshift independent dust opacity is assumed to be an average Galactic interstellar extinction law normalized at the V-band to match this observed extinction. D98 then calculate the EBL spectrum using the UV-optical observed _*(z), a Salpeter IMF (0.1 < M < 120 M), stellar evolutionary tracks from Bressan et al. (1993), Kurucz stellar atmosphere models for solar metallicity, redshift-independent dust extinction, and dust re-emission matching the SED of IRAS galaxies.

The starting-point UV-optical _*(z) for this model is taken from Madau, Pozzetti, & Dickinson (1998), which under-predicts the detected optical EBL presented in Paper I (see Section 4.3). While D98 discuss two models which include additional star formation at z 1, the additional mass is all in the form of massive stars which radiate instantaneously and are entirely dust-obscured, resulting in an ad hoc boost to the far IR-EBL. We instead simply scale the initial Dwek et al. model by × 2.2 to match the 2 lower limit of our EBL detections and × 4.7 to match the 2 upper limit, in order to preserve the consistency of the D98 model with the observed spectral energy density at z = 0. In that any emission from z > 1 will have a redder spectrum than the mean EBL, simply scaling in this way will produce a spectrum which is too blue. However, as discussed in Section 4.2, it is also possible that the z < 0.5 UV luminosity density has been underestimated by optical surveys, so that the bluer spectrum we have adopted may be appropriate. Note that the resulting model is in excellent agreement with recent near-IR results at 2.2 and 3.5µm (Wright & Reese 2000; Gorjian, Wright, & Chary 2000; Wright 2001) and also with the DIRBE and FIRAS results in the far-IR. Adopting this model, we estimate that the total bolometric EBL is 100±20 nW m^-2sr^-1, where errors are 1 errors associated with the fit of that template to the data.

Due to the corrections which account for the redistribution by dust of energy into the IR portion of the EBL, the star formation rate implied by the unscaled (or scaled) D98 model is 1.5 (or 3.3-7.1) times larger than the star formation rate adopted by Madau et al. (1998). The dust corrections used by Steidel et al. (1999) produce a star formation rate which is roughly 3 times larger than used in the unscaled D98 model, slightly smaller than the scaling range adopted here, which is consistent with the fact that the CFRS and Steidel et al. (1999) luminosity densities are slightly below our minimum values for the EBL, as discussed in Section 4.2.