Annu. Rev. Astron. Astrophys. 1988. 26: 509-560 Copyright © 1988 by Annual Reviews. All rights reserved

4.2. Field Galaxies

Felten (1977) has reviewed the classical determinations of the field LF by Kiang (1961), van den Bergh (1961), Holmberg (1969), Arakelyan & Kalloglyan (1970), Shapiro (1971), Huchra & Sargent (1973), Christensen (1975), Turner & Gott (1976b), and Schechter (1976). He concluded that the available data could be fitted reasonably well with a Schechter function with = -1.25 and M_BT^* = -21.0. The exception is the LF of groups as set out by Turner & Gott (1976b), who required a faint-end slope of ~ -1. This is interesting because all later determinations of the field LF point to a similarly shallow faint-end slope. Although this is a very important question concerning the frequency of true dwarfs in the field, too much weight should not be given to Turner & Gott's conclusion because their group data do not constitute a well-defined sample. Similarly, the unusual LFs found by White & Valdes (1980) for binaries and Heiligman & Turner (1980) for compact groups are suspected to be caused by the sample selection. In our opinion this crucial question of the faint-end slope of the LF for groups is yet to be solved.

Felten's (1977) review can be considered to be a demarcation line between eras. Two subsequent developments initiated the postclassical period of the field LF studies. First, new samples were defined. In addition to the Reference Catalog of Bright Galaxies (de Vaucouleurs & de Vaucouleurs 1964) and later the RC2 (de Vaucouleurs et al. 1976), the magnitude-limited all-sky redshift sample of the RSA also became available, as did the deep sample of the Harvard Center for Astrophysics with a wide sky coverage (the CfA survey of Huchra et al. 1983). Furthermore, two deep pencil-beam redshift samples were completed by Kirshner et al. (1978; the KOS sample) and by Ellis (1983) and Peterson et al. (1986; known as the Durham/AAT sample). Second, by uncovering the inhomogeneous spatial distribution of galaxies, these new redshift surveys led to the refined methods described in Section 3.

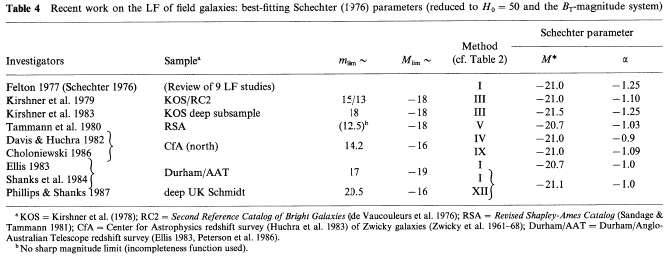
Those Schechter parameters of the field LF that are independent of the assumption of constant space density are set out in Table 4. To reduce the various results to the B_T system, the transformations of Felten (1985) have been adopted. As seen from Table 4, the post-1977 investigations, with the exception of that of Kirshner et al. (1983), lead consistently to a flatter faint-end slope with ~ -1.0 as opposed to ~ 1.25 for clusters (Section 4.1). As shown below, this difference of the dwarf-to-giant ratio is a natural consequence of the different type mixture in clusters and in the field. On the other hand, M_BT^* remains stable at ~ -21. The previously steeper slopes may be caused by the local density enhancement. Yet Felten (1985) argues that the flat slope obtained by Davis & Huchra (1982) is due to the admittedly imprecise Zwicky magnitudes. Nevertheless, the evidence is mounting for ~ -1.0 in the field, which would be proof that the ratio of dwarfs to giants depends on the environmental density. This, if true, would be a fundamental result, but again we believe the jury is still out on this matter.