Annu. Rev. Astron. Astrophys. 1988. 26: 509-560 Copyright © 1988 by Annual Reviews. All rights reserved

3. METHODS TO DETERMINE THE LUMINOSITY FUNCTION

Galaxies are usually divided into "cluster galaxies" and "field galaxies." A "cluster galaxy" is a member of a (rich) cluster that is representative of the clusters listed in, for example, Abell's (1958) or Zwicky et al.'s (1961-68) catalogs of clusters. As "field galaxy," one can then simply declare as such every galaxy that is not lying in a (rich) cluster; groups of galaxies thus become part of the "field." This conventional definition of a field galaxy (e.g. Felten 1977) is adopted here. The distinction between clusters and field is natural in the context of the luminosity function because the methods used to derive a LF for a cluster and for a field sample are fundamentally different. In the former case, all galaxies are at the same distance; in the latter, individual distances must be known (groups of galaxies excepted). "Cluster" and "field" also denote two basic density environments of galaxies, whose LFs cannot be expected to be the same a priori. Therefore the "cluster" and the "field" LFs are treated separately in this and the following section. All methods used to determine the LF discussed here are based on the assumption that the LF does not depend on galaxian position (within the cluster, or in the field). This means that and D can be separated, as expressed by Equation 8. This conventional approach is challenged in Section 6, where a general "LF-density relation" is proposed.

3.1. Cluster Galaxies

Because all cluster galaxies are at the same distance, the apparent magnitudes m, after appropriate binning, are used directly to give (m) as a histogram. If the sampling has been proper, the distribution will be complete to a certain limiting magnitude m_lim. Scaling by the distance modulus of the cluster (inferred, for example, from the redshift) transforms (m) into (M) and m_lim into M_lim. The difficulty is to identify the cluster members among the great number of galaxies that are always projected into the same area of the sky.

Ideally, many of the cluster members betray themselves from their morphological types. Such a morphological sampling has proved possible for the nearby clusters in Virgo (BST, Sandage et al. 1985; hereinafter SBT) and Fornax (Ferguson & Sandage 1987), which have recently been mapped with high angular resolution. The method is based on the galaxian characteristics of surface brightness at a given magnitude, and resolution into H II regions and associations, both of which can be used as relative distance indicators (BST). For example, intrinsically faint members of a cluster (with the exception of blue compact dwarf galaxies (the BCDs)] are of low surface brightness. whereas typical (intrinsically bright) background galaxies have high surface brightness. Only early-type giant (E and S0) and BCD galaxies are difficult to identify as cluster members, as they have high surface brightness and show little structural detail. Here one is forced to use velocity data to determine cluster membership. Moreover, both the morphological and kinematical criteria work reliably only if a cluster is fairly isolated in space. This is because there is cosmic scattering of the morphological characteristics, and the velocities are dispersed by ~ 1000 km s^-1 around the cluster mean, making velocity discrimination unsharp unless there is a spatial void behind the cluster. Fortunately, many clusters (like the Virgo cluster) meet this requirement because they are in front of large voids (Sulentic 1980, Davis et al. 1982, Ftaclas et al. 1984), and hence the background contamination is minimal. Even so, there always remains a fraction of the cluster sample for which membership cannot be decided with total certainty (of the order of 10% in the Virgo cluster; BST).

If the cluster members cannot be identified on morphological grounds, the second best procedure is to sample solely by velocity. To date, this has implied a restriction to bright galaxies. Dwarf galaxies, which mostly have low surface brightness, can only be sampled morphologically at present. LF studies based on pure velocity sampling have been carried out for the Fornax cluster by Jones & Jones (1980) and for the Virgo cluster by Kraan-Korteweg (1981).

The normal case in cluster LF studies, however, has been a poor morphological resolution of the galaxies with velocity data available only for a small subsample of bright galaxies. At present, this situation applies to all clusters that are more distant than Virgo and Fornax. The identification of cluster members against foreground and background galaxies (or even stars) can be achieved only in a statistical way for the more distant clusters. In order to clean a cluster sample of the contamination by field galaxies, one must determine the number of field galaxies in a given magnitude bin that are expected to be randomly projected onto the cluster area [usually given as log N(m), where N(m) is the number of galaxies that are brighter than apparent magnitude m]. These numbers are then subtracted from the uncorrected cluster LF. The log N(m) values can be determined either locally by going to a field near the cluster or by adopting an average log N(m) law. For the faintest magnitude bins, a similar correction must be applied for possible contamination from stars (see Austin & Peach 1974) if the survey is made with inadequate angular resolution. A type-dependent correction for field contamination so as to differentiate cluster LFs by type (Thomson & Gregory 1980) must make specific allowance for the type-density relation (cf. Section 6.1.). The most widely used log N(m) curve in cluster studies (e.g. Dressler 1978, Lugger 1986, Oegerle et al. 1986, 1987) is that of Oemler (1974), who constructed a mean log N(m) law from galaxy counts in several fields near his clusters. However the nonuniformity of the distribution of "field" galaxies is now generally acknowledged (e.g. Davis et al. 1982), and it must be doubted whether a field correction based on a general log N(m) law is meaningful in all cases. There certainly are clusters where a local log N(m) must be used (see Dressler 1978). Cluster LFs that are corrected only statistically for background contamination are uncertain principally at the faint end, where often the field counts to be subtracted reach the same order of magnitude as the cluster counts.

Once a corrected cluster LF is established, a useful representation is that of Schechter (1976) in the form

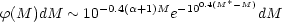
(13)

corresponding to

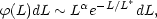
(14)

where and M^* (or L^*) are free parameters. This function has superseded other analytic expressions used previously by Zwicky (1957), Kiang (1961), and Abell (1962, 1965), which are not further discussed in this review. At faint magnitudes, Equation 13 is exponential with slope -0.4( + 1). On the bright side, it is a double exponential that rapidly approaches zero after a turnover at a characteristic magnitude M^* (corresponding to a characteristic luminosity L^*). Because of the definition (M) in Section 2, the normalization of the Schechter function is not considered. For normalization via the local density function, see Schechter (1976).

The best-fit parameters and M^* for a cluster LF can be found by minimizing ² in fitting Equation 13 to the binned magnitude data (e.g. Dressler 1978). A generalized ² statistic to include the uncertainty in the background correction has been used by Lugger (1986). Alternatively, one can apply a maximum-likelihood method to the unbinned data to obtain and M^* (Lugger 1986, Oegerle et al. 1986).